Geometria Maciek: Przez punkt O, leżący wewnatrz trojkata ABC poprowadzono 3 proste równoległe do boków trojkata. Te proste podzielily ten trojkąt na 6 czesci, z których trzy są trójkątami. Udowodnij, że jeżeli r1, r2, r3 są promieniami okręgów wpisanych w te trójkąty, a r jest promieniem okręgu wpisanego w trójkąt ABC to: r1+r2+r3=r

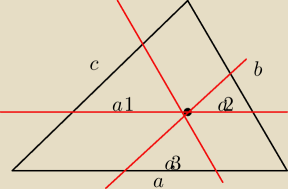
Basia: skoro proste są równoległe wszystkie trójkąty są podobne

	a1
T1~T w skali		=k1
	a

	a2
T2~T w skali		=k2
	a

	a3
T3~T w skali		=k3
	a

a₁+a₂+a₃=a obwody są podobne w tych samych skalach pola w ich kwadratach stąd

	2P1		2k12*P		2P
r1 =		=		= k1*		= k1*r
	L1		k1*L		L

r₂ = k₂*r r₃ = k₃*r

	a1		a2		a3
r1+r2+r3 = (k1+k2+k3)*r = (		+		+		)*r =
	a		a		a

a1+a2+a3		a
	*r =		*r = r
a		a