Badanie przebiegu zmiennosci funkcji
spanikowany: Bylby ktos tak mily i lopatologicznie przeprowadzil badanie tej funkcji? Z uwzglednieniem
operacji na liczbie e (wyciaganie minusa przed liczbe itd)
f(x)= (x+1)*e−x
Moze jest gdzies podobny przyklad? Szukalem ale nic mi nie wpadlo w oko.
3 sty 21:01
Basia:
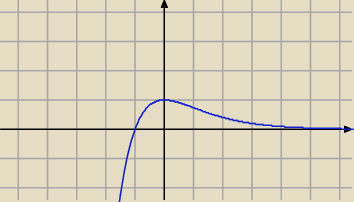
D=R
lim
x→−∞f(x) = lim
x→−∞(x+1)*e
−x = (−
∞)*e
−(−∞) = (−
∞)*(+
∞) = −
∞
| | x+1 | | 1 | | 1 | |
limx→+∞f(x) = limx→+∞ |
| = limx→+∞ |
| = [ |
| ]=0 |
| | ex | | ex | | +∞ | |
czyli masz asymptotę poziomą prawostronną y=0
f'(x) = (x+1)'*e
−x + (x+1)*(e
−x)' = 1*e
−x + (x+1)*e
−x*(−x)' =
e
−x+(x+1)*e
−x*(−1) = e
−x − (x+1)e
−x = e
−x(1−x−1) = −x*e
−x
f'(x) = 0 ⇔ x=0
x<0 ⇒ −x>0 ⇒ f'(x)>0 ⇒ f rośnie
x>0 ⇒ −x<0 ⇒ f'(x)<0 ⇒ f maleje
czyli dla x=0 funkcja osiąga maksimum = f(0)=(0+1)*e
−0 = 1*e
0 = 1*1 = 1
wklęsłość i wypukłość też potrzebne?
3 sty 21:22
spanikowany: gdybys jeszcze obliczyla wkleslosc i wypuklosc to tak ozlocilbym Cie

ps Przepraszam za brak polskich znakow
3 sty 21:42
spanikowany: a parzystosc i nieparzystosc?
3 sty 21:44
Basia: no przecież już z przebiegu zmienności gołym okiem widać, że nie jest ani parzysta, ani
nieparzysta
4 sty 00:25
Basia:
| | 1*ex−x*ex | | ex(x−1) | | (x−1) | |
f"(x) = − |
| = |
| = |
| |
| | (ex)2 | | ex*ex | | ex | |
f"(x)=0 ⇔ x−1=0 ⇔ x=1
x∊(−
∞;1) ⇒ x−1<0 ⇒ f"(x)<0 ⇒ f jest wklęsła
x∊(1;+
∞) ⇒ x−1>0 ⇒ f"(x)>0 ⇒ f jest wypukła
dla x=1 mamy punkt przegięcia
4 sty 00:30
 D=R
D=R
 ps Przepraszam za brak polskich znakow
ps Przepraszam za brak polskich znakow