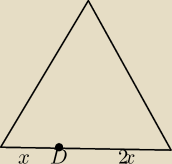Punkt D dzieli podstawę trójkąta równobocznego o boku a w stosunku 1:2. Oblicz odległości
punktu D od ramion tego trójkąta
| d1 | |
= cos 30o | |
| x |
| √3 | 1 | √3 | √3 | |||||
d1 = x* | = | a* | = a | |||||
| 2 | 3 | 2 | 6 |
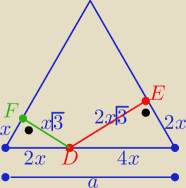
| a | ||
a=6x ⇒ x= | ||
| 6 |
| a√3 | ||
|DE|=2x√3= | ||
| 3 |
| a√3 | ||
|DF|=x√3 = | ||
| 6 |
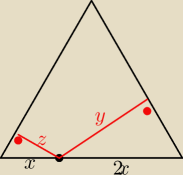
| a | ||
dane jest a (czyli długość boku trójkąta) to x= | 2x=U{2a}[3} | |
| 3 |
| y | ||
sin60 = | ||
| 2x |
| z | ||
sin60 = | ||
| x |
| 2a | √3 | a√3 | ||||
y = 2x*sin60 = | * | = | ||||
| 3 | 2 | 3 |
| a | √3 | a√3 | ||||
z = x*sin60 = | * | = | ||||
| 3 | 2 | 6 |
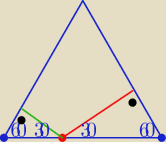Zapomniałam zaznaczyć miary kątów na poprzednim rys.