 Dane są dwa okręgi o średnicach AS i BS oraz okrąg o średnicy AB i środku S. Okrąg o środku M i
promieniu r jest styczny do każdego z danych okręgów. Uzasadnij, że AB=6r.
Dane są dwa okręgi o średnicach AS i BS oraz okrąg o średnicy AB i środku S. Okrąg o środku M i
promieniu r jest styczny do każdego z danych okręgów. Uzasadnij, że AB=6r.
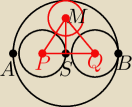 AB=x
AB=x
| 1 | x | |||
PS=QS = | AB= | |||
| 4 | 4 |
| 1 | ||
PM+QM = | AB+r = U{x}[4}+r | |
| 4 |
| 1 | x | |||
MS = | AB−r = | −r | ||
| 2 | 2 |
| x2 | x | x | |||
+ ( | −r)2 = ( | +r)2 | |||
| 16 | 2 | 4 |
| x2 | x2 | x2 | rx | ||||
+ | − rx + r2 = | + | +r2 | ||||
| 16 | 4 | 16 | 2 |
| x2 | rx | ||
− rx = | /*4 | ||
| 4 | 2 |
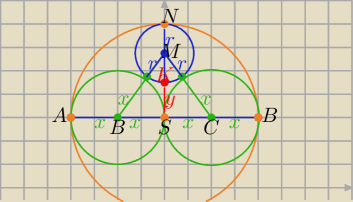 |AB|=4x , |MS|=r+y , |MN|=2x=2r+y ⇒ y=2x−2r i |BM|=x+r
Z tw. Pitagorasa w ΔBSM
(x+r)2= x2+(r+y)2 ⇒(x+r)2=x2+(2x−r)2
2rx = 4x2−4rx / : x>0 ⇒ 4x=6r
to |AB|=6r
c.n.w
|AB|=4x , |MS|=r+y , |MN|=2x=2r+y ⇒ y=2x−2r i |BM|=x+r
Z tw. Pitagorasa w ΔBSM
(x+r)2= x2+(r+y)2 ⇒(x+r)2=x2+(2x−r)2
2rx = 4x2−4rx / : x>0 ⇒ 4x=6r
to |AB|=6r
c.n.w