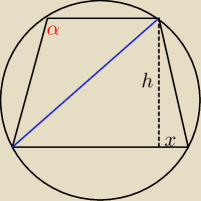
 h2 + (a+x)2 = 172
h2 + x2 = b2
2(a+x+b) = 60
172 = a2 + b2 − 2abcosα
172 = (a+2x)2 + b2 − 2(a+2x)bcos(180−α) ⇔ 172 = (a+2x)2 + b2 + 2(a+2x)bcosα
układ 5 równań z 5−cioma niewiadomymi
h2 + (a+x)2 = 172
h2 + x2 = b2
2(a+x+b) = 60
172 = a2 + b2 − 2abcosα
172 = (a+2x)2 + b2 − 2(a+2x)bcos(180−α) ⇔ 172 = (a+2x)2 + b2 + 2(a+2x)bcosα
układ 5 równań z 5−cioma niewiadomymi
 Zaraz namaluję
Zaraz namaluję 
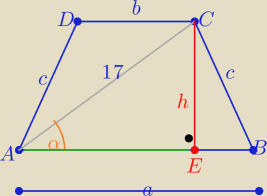 1/ z warunku wpisania okręgu w trapez
1/ z warunku wpisania okręgu w trapez
| a+b | ||
a+b=2c to L= 2a+2b =60 ⇒ | =15 =|AE| i c=15 | |
| 2 |
| 8 | ||
h=√172−|AE|2= .. h=8 i sinα= | ||
| 17 |
| a+b | ||
P= | *h= .............. | |
| 2 |
| c | ||
2R= | = ..... | |
| sinα |