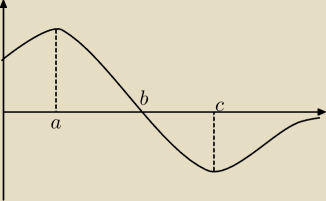
przebieg zmiennosci pochodnej pppp: Bardzo proszę o pomoc: Określ przebieg zmienności funkcji będącej pochodną funkcji f(x), której wykres jest przedstawiony na rysunku. (Dla jakich argumentow pochodna funkcji f(x) jest funkcja o dodatnich wartosciach, dla jakich o ujemnych wartosciach, dla jakich funkcja rosnaca i dla jakich malejaca). Uzasadnij odpowiedź

kochanus_niepospolitus: f'(x) > 0 dla (0;a) oraz (c; d) oraz (d, +∞) f'(x) < 0 dla (a,c) bo w tych przedziałach funkcja jest rosnąca / malejąca Punkt d to punkt na prawo od punktu c, gdzie mamy widoczny punkt przegięcia (wtedy także możliwe, że f'(x) = 0)

Basia: D = R₊ x∊<0; b) ⇒ f'(x)>0 ⇒f rośnie x∊(b;+∞) ⇒ f'(x)<0 ⇒ f maleje

Basia: aj, źle przeczytałam, myślałam, że na wykresie jest pochodna

kochanus_niepospolitus: chwila chwila ... to jest wykres f(x) czy f'(x)

kochanus_niepospolitus: Basiu ... a ja właśnie teraz zacząłem się zastanawiać czy to nie jest wykres pochodnej

pppp: to jest wykres f(x)

kochanus_niepospolitus: no to patrzaj co ja mam napisane ... gdyby to był wykres f'(x) to by Basi odpowiedź była odpowiednia.