Planimetria
Satan: Dany jest prostokąt ABCD i dowolny punkt K położony we wnętrzu prostokąta. Wykaż, że |AK|
2 +
|CK|
2 = |BK|
2 + |DK|
2
Więc tak. Najprostszą drogą jest obranie punktu K na przecięciu się przekątnych tego
prostokąta, udowodnienie przystawania trójkątów, dopowiedzenie, że przekątne składają się z
tych odcinków i to jest proste. Ale jak to rozwiązać, gdy obejmiemy sobie punkt K gdzie
indziej? Na przykład tak, by każdy odcinek z odcinków wyżej wymienionych leżał na innej
prostej.
Pomysły mile widziane


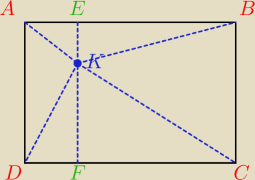 z tw. Pitagorasa
|AK|2=|AE|2+|EK|2
|BK|2=|EK|2+|EB|2
|CK|2=|KF|2+|FC|2
|DK|2=|KF|2+|DF|2
|EB|=|FC|
|AE|=|DF|
stąd mamy tezę
z tw. Pitagorasa
|AK|2=|AE|2+|EK|2
|BK|2=|EK|2+|EB|2
|CK|2=|KF|2+|FC|2
|DK|2=|KF|2+|DF|2
|EB|=|FC|
|AE|=|DF|
stąd mamy tezę

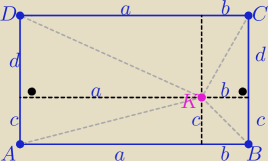 |AK|2+|CK|2= a2+c2+b2+d2
|BK|2+|DK|2=b2+c2+a2+d2
zatem |AK|2+|CK|2=|BK|2+|DK|2
c.n.w
|AK|2+|CK|2= a2+c2+b2+d2
|BK|2+|DK|2=b2+c2+a2+d2
zatem |AK|2+|CK|2=|BK|2+|DK|2
c.n.w
