dziedzina funkcji
5-latek: Znalezc dziedzine funkcji okreslonej na przedziale <0,1>
f(tgx)
f(x−5)
Jesli sobie wprowadze pomocniczy argument u=tgx to ma f(tgx)= f(u) jest okreslona gdy 0≤u≤1
0≤tgx≤1 wiec
kπ≤x≤π/4+kπ k∊C
Jedna mam tutaj watpliwosc co do tego rozwiazania . Kazano postepowac analogicznie ja w
innym przykladzie
wiec tak zrobilem ale przeciez przedzial na osi liczbowej <0,1> jest jeden to po co to kπ?
wedlug mnie powinno byc
0≤x≤π/4
Jak zrobic ten przyklad nr 2
2 sty 17:14
5-latek: czy dla f(x−5) bedzie tak
0≤x−5≤1
0−5≤x≤1+5
−5≤x≤6
2 sty 17:19
5-latek: Blad
5≤x≤6
========
2 sty 17:40
5-latek:
2 sty 19:15
iteRacj@:
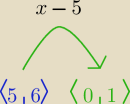
tak,
jeśli dziedziną f(x) jest <0,1>, to dziedziną f(x−5) będzie <5,6>
rysunek mało przydatny, ale to takie ćwiczenie w rysowaniu
2 sty 19:36
5-latek: Dobry wieczor
iteRacj@ 
Tak . Ale bardziej chodzi mi o moja watpliwoasc z 1 postu .
2 sty 20:16
Adamm: powiem ci że ta wątpliwość jest nieuzasadniona
jeśli szukamy "dziedziny" to chodzi nam o największy podzbiór zbioru liczb rzeczywistych
dla którego f(tgx) może być określone
wybierając jedynie jeden przedział jako dziedzinę, ograniczamy ją
2 sty 20:19
5-latek:
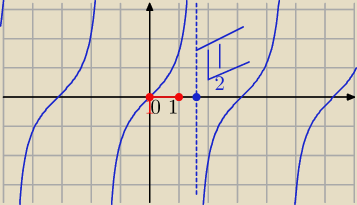
czesc
Adamm 
ale zobacz tutaj mamy ten przedzial
2 sty 20:29
iteRacj@:
masz funkcję złożoną, wewnętrzna to tg(x), zewnętrzna to f(tg(x))
dziedzina f. wewnętrznej ma być tak dobrana, żeby zbiór wartości, które "wytworzy" ta funkcja,
zawierał się w dziedzinie f. zewnętrznej
skoro argumenty, spełniające warunek kπ≤x≤π/4+kπ k∊C, "trafiając" do funkcji tg(x), dają
wartości z żądanego przedziału <0,1>, to jak najbardziej są odpowiednie
2 sty 20:34
5-latek: Dobrze . Rozumiem juz
2 sty 20:38
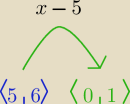 tak,
jeśli dziedziną f(x) jest <0,1>, to dziedziną f(x−5) będzie <5,6>
rysunek mało przydatny, ale to takie ćwiczenie w rysowaniu
tak,
jeśli dziedziną f(x) jest <0,1>, to dziedziną f(x−5) będzie <5,6>
rysunek mało przydatny, ale to takie ćwiczenie w rysowaniu
 Tak . Ale bardziej chodzi mi o moja watpliwoasc z 1 postu .
Tak . Ale bardziej chodzi mi o moja watpliwoasc z 1 postu .
 czesc Adamm
czesc Adamm  ale zobacz tutaj mamy ten przedzial
ale zobacz tutaj mamy ten przedzial