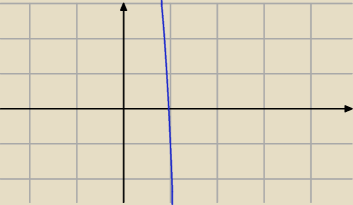
Pochodne wixa04: Udowodnij, że równanie −7x⁵+4x³−7x=−9 ma conajmniej jedno rozwiązanie w przedziale (−1,0)

PW: W(x)=−7x⁵+4x³−7x+9 W(−1)=7−4+7+9 =19 W(0)=9. W'(x)=−35x⁴+12x²−7 Δ<0 − W'(x) jest ujemna dla wszystkich x, a więc W(x) jest malejąca, w szczególności maleje na przedziale [−1,0] przyjmując wartości od 19 do 9. Wniosek: w przedziale (−1,0) nie ma miejsc zerowych. Pewnikiem w poleceniu miał być przedział (0,1).