matematykaszkolna.pl
zadanie qqq: rozwiaz nierowność 2cosx−√3/cos2x <0
1 sty 22:38
qqq: czy to bedzie x∊(π/2+2kπ;3/2π+2kπ) ?
1 sty 22:39
qqq: czy mogłby ktoś sprawdzić , uprzejmie prosze
1 sty 22:40
qqq:
1 sty 22:43
Qulka: nie bardzo dobrze http://www.wolframalpha.com/input/?i=(2cosx%E2%88%92%E2%88%9A3)%2Fcos%5E2x+%3C0+from+0+to+2pi
1 sty 22:46
qqq: nie rozwiazujemy tego jako nierowność wymierna ?
1 sty 22:54
Qulka: nie musisz.. mianownik jest kwadratem więc na pewno nie będzie ujemny
1 sty 22:56
qqq: tak sie szuka pierwiastkow rozwiazania czy nie ?
1 sty 22:58
Qulka: gdy cosx=√3/2 więc dla 30° lub 150°
1 sty 23:06
qqq: √3/2 = 0.866025 czyli x=π/6 i x=11/6π
1 sty 23:13
qqq: dobra juz wiem dzieki
1 sty 23:14
Basia: czy to jest tak?
 √3 
2cosx −
< 0
 cos2x 
1 sty 23:15
Basia: czy raczej po prostu tak:
2cosx−√3 
<0
cos2x 
1 sty 23:15
qqq: tak jak podane wyzej
1 sty 23:16
qqq: drugie
1 sty 23:16
Basia: rysunek
 π 
założenie: cosx≠0 ⇔ x≠±
+2kπ
 2 
poza tym cos2x > 0 czyli musi być 2cosx−√3<0
 √3 
cosx<
 2 
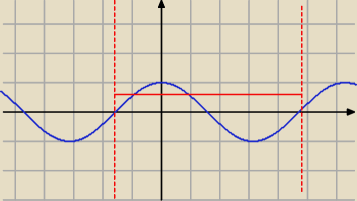
 √3 π 
w zaznaczonym przedziale cosx=
dla x=±
 2 6 
 π π π 3π 
czyli mniejsze jest (−
; −
)∪(
;
)
 2 6 6 2 
mamy wobec tego:
 π π π 3π 
x∊(−
+2kπ; −
+2kπ)∪(
+2kπ;
+2kπ)
 2 6 6 2 
1 sty 23:25
qqq: w przedziale <0;2π> ma byc ta nierówność
1 sty 23:29
Qulka: w normalnym zakresie chyba byłoby łatwiej zapisać (π/6 +2kπ ; 11π/6 +2kπ)
1 sty 23:29
Qulka: qqq to po co podawałeś z kπ
1 sty 23:30
qqq: racja dzieki
1 sty 23:34
qqq: to jaki ostatecznie przedzial ?
1 sty 23:51
qqq:
2 sty 00:03