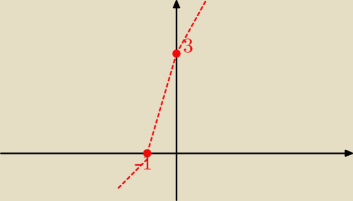
Rysunek przedstawia fragment wykresu pewnej Bela: to jest parabola... Rysunek przedstawia fragment wykresu pewnej funkcji kwadratowej f. Prosta o równaniu x=−2 jest osią symetrii paraboli. a)naszkicój wzór określający funkcję f. b) naszkicuj wykres funkcji y=f(|x|) c) uzasadnij, że równanie f(x)+ (m+1)x−4=0 ma dwa rozwiązania kazdej wartości parametru m.

dsa: y=a(x−p)2−q p=−2 nie wiem jak a i q wykombinować o;

Patryk:

−1+b
	=−2 b=drugie miejsce zerowe
2

adaś: a)

⎧	f(0) = 3
⎨	f(−1)=0
⎩	f(x)=a(x+2)2+q

⎧	3=a(0+2)2+q
⎨	f(−1)=0
⎩	f(x)=a(x+2)2+q

⎧	q=3−4a
⎨	0=a+3−4a
⎩	f(x)=a(x+2)2+q

⎧	q=3−4a
⎨	0=a+3−4a
⎩	f(x)=a(x+2)2+q

⎧	q=3−4a
⎨	−3=−3a⇒a=1
⎩	f(x)=a(x+2)2+q

⎧	q=3−4a⇒q=−1
⎨	a=1
⎩	f(x)=a(x+2)2+q

⎧	q=−1
⎨	a=1
⎩	f(x)=1(x+2)2−1

c.n.u

Sławek: f(x)=a(x−x₁)(x−x₂) f(0)=3 f(0)=a(0+1)(0+2) 3=a(0+1)(0+2) 3=3a a=1 f(x)=(x+1)(x+2) f(x)=x²+3x+2

adaś: ale to ma być parabola D;

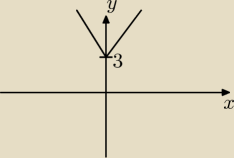
adaś: b) y=f(|x|) y=(|x|+2)²+3 y=x²+4|x|+3 ⇒x=0 y=3

adaś: c) [(x+2)² −1] + (m+1)x−4=0 x²+4x+4−1+mx+x−4=0 x²+5x+mx−1=0 x²+x(5+m)−1=0 Δ_x=(m+5)²−4*1*(−1) Δ_x=m²+10m+29 Δ_m=100−116=−16 Δ_m<0 ⇒ m ∊ R

Trivial: Parabole tańczą, tańczą, tańczą, tańczą, tańczą, tańczą, tańczą parabole...

:D: no way

:D: