Podaj przykład takiej funkcji
CR: Podaj przykład takiej funkcji ψ : R → R, że dla każdego r∈R zbiór ψ−1[{r}] , ma dokładnie 2
elementy
1 sty 18:14
g: To może być tg(x) ale z ograniczoną dziedziną x ∊ (−π/2, π/2) ∪ (π/2, 3π/2).
1 sty 18:38
Basia: chyba nie możemy ograniczać dziedziny, to byłoby zbyt proste
np. y=x2 ale w dziedzinie R\{0}
1 sty 18:48
Basia: a nie sorry ma być dla kazdego r∊R
1 sty 18:49
CR: A funkcja logarytmiczna z wartosia bezwględną w x?
1 sty 19:27
Adamm:
dla (−∞; 0)
f(x)=−x dla x≤1
−1/x dla x>1
dla [0;∞)
tutaj próbuję znaleźć jakąś bijekcję na R, ale brak pomysłów
1 sty 20:00
Adamm: poprawka
f(x)=x dla x≤1
1 sty 20:01
Adamm:
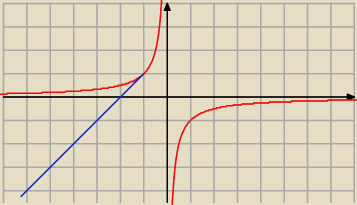
poprawka
f(x)=x+1 dla x≤2

1 sty 20:02
Adamm: x≤1
1 sty 20:02
Adamm:
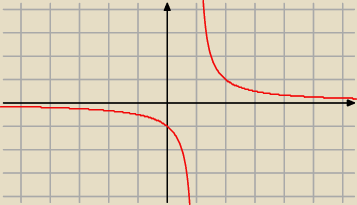
dla [0,
∞) zbudujmy ją tak
f(0)=0
dla (0, 1]
f(x)=1/x
dla (1, 2]
f(x)=−1/(x−1)
dla (2, 3]
f(x)=1/(x−1)
i tak dalej
taka funkcja jest bijekcją [0,
∞) na R
czyli podaliśmy przykład takiej funkcji
1 sty 20:09
Basia: dla jakiego jeszcze argumentu masz wartość 0?
1 sty 20:41
Adamm: −1
1 sty 20:42
Adamm: nie, −2
a tam się pomyliłem jeszcze bardziej
f(x)=x+2 dla x≤−1
−1/x dla x>−1
1 sty 20:43
Basia:
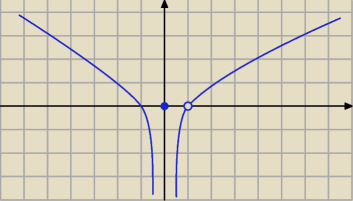
coś takiego
1 sty 20:51
Basia: czyli mogłoby być tak:
y =ln|x| dla x<0
y = 0 dla x=0
y= lnx dla x∊(0,1)∪(1;+∞)
1 sty 20:53
mat: a co z f(1)?

1 sty 20:54
Basia: fakt, wtedy nie istnieje f(1);
1 sty 21:22
Basia:
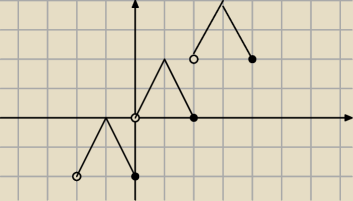
coś takiego? czy jeszcze coś nie tak? rozpisać to się da, ale nie wiem czy warto

1 sty 21:30
CR: Basia a tą ostatnią funkcje jak rozpisać? ^^
1 sty 21:50
Basia:
zauważ, że
f(x) = 2x dla x∊(0,1)
= −2x+4 dla x∊<1,2>
a potem przesuwamy przedziały o 2k, natomiast wykresy o wektor [2k;2k]
otrzymujemy
f(x) = 2(x−2k)+2k = 2x − 2k dla x∊(2k;2k+1)
= −2(x−2k)+4+2k = −2x+6k+4 dla x∊<2k+1;2k+2>
da się trochę łatwiejszą funkcję wymyślić; zamiast 2x wziąć x, zamiast −2x wziąć −x
1 sty 22:31
CR: Wygląda na to że to dobra funkcja

wielkie dzięki Basia ^^
1 sty 22:54
 poprawka
f(x)=x+1 dla x≤2
poprawka
f(x)=x+1 dla x≤2 
 dla [0, ∞) zbudujmy ją tak
f(0)=0
dla (0, 1]
f(x)=1/x
dla (1, 2]
f(x)=−1/(x−1)
dla (2, 3]
f(x)=1/(x−1)
i tak dalej
taka funkcja jest bijekcją [0, ∞) na R
czyli podaliśmy przykład takiej funkcji
dla [0, ∞) zbudujmy ją tak
f(0)=0
dla (0, 1]
f(x)=1/x
dla (1, 2]
f(x)=−1/(x−1)
dla (2, 3]
f(x)=1/(x−1)
i tak dalej
taka funkcja jest bijekcją [0, ∞) na R
czyli podaliśmy przykład takiej funkcji
 coś takiego
coś takiego

 coś takiego? czy jeszcze coś nie tak? rozpisać to się da, ale nie wiem czy warto
coś takiego? czy jeszcze coś nie tak? rozpisać to się da, ale nie wiem czy warto
 wielkie dzięki Basia ^^
wielkie dzięki Basia ^^