BARDZO PROSZĘ O POMOC
Miki: 1.Punkty A,B,C,D leżące na płaszczyźnie spełniającej warunki: punkt B jest środkiem odcinka AC,
przy czym AB=BC=BD=17 oraz AD=16.Oblicz długość odcinka CD.
2. Oblicz NWD( n2+6, n+1). Odpowiedź uzasadnij.
3. Załóżmy,że wybrano 30 punktów w kwadracie o boku 10. Udoowodnij,że wewnątrz kwadratu
istnieje punkt odległy od każdego z wybranych punktów o więcej niż 1.
4.Dany jest prostokąt i kwadrat o takim samym polu. Pokaż,jak podzielić jedną z tych figur na
części i złożyć z tych części drugą figurę.
1 sty 17:55
iteRacj@:
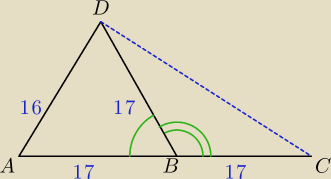
z tw. cosinusów dla ΔABD
16
2 = 17
2 +17
2 − 2*17*cosα
stąd 2*17*cosα = 2*17
2 −16
2
z tw. cosinusów dla ΔCBD
|CD|
2 = 17
2 +17
2 − 2*17*cos(180
o−α)
|CD|
2 = 17
2 +17
2 + 2*17*cosα
|CD|
2 = 17
2 +17
2 −16
2 + 17
2 +17
2
|CD|
2 = 4*17
2 −16
2 = 900
stąd |CD|=30
1 sty 19:11
Eta:
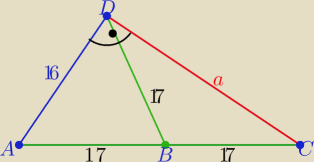
Trójkąt ADC jest prostokątny bo jest wpisany w okrąg o promieniu R=17 i średnicy |AC|=34
to |DC|=
√342−162=
√900=
30
1 sty 19:47
1 sty 19:51
 z tw. cosinusów dla ΔABD
162 = 172 +172 − 2*17*cosα
stąd 2*17*cosα = 2*172 −162
z tw. cosinusów dla ΔCBD
|CD|2 = 172 +172 − 2*17*cos(180o−α)
|CD|2 = 172 +172 + 2*17*cosα
|CD|2 = 172 +172 −162 + 172 +172
|CD|2 = 4*172 −162 = 900
stąd |CD|=30
z tw. cosinusów dla ΔABD
162 = 172 +172 − 2*17*cosα
stąd 2*17*cosα = 2*172 −162
z tw. cosinusów dla ΔCBD
|CD|2 = 172 +172 − 2*17*cos(180o−α)
|CD|2 = 172 +172 + 2*17*cosα
|CD|2 = 172 +172 −162 + 172 +172
|CD|2 = 4*172 −162 = 900
stąd |CD|=30
 Trójkąt ADC jest prostokątny bo jest wpisany w okrąg o promieniu R=17 i średnicy |AC|=34
to |DC|=√342−162=√900= 30
Trójkąt ADC jest prostokątny bo jest wpisany w okrąg o promieniu R=17 i średnicy |AC|=34
to |DC|=√342−162=√900= 30