dowód w sześcianie house: Mam problem z zadaniem 11 z rozszerzonej matury z 2016 z czerwca. Dodałem tam komentarz, ale nie wiem czy ktokolwiek odwiedza to miejsce. Na stronie 4743. Skąd mam wiedzieć, że punkt P leży na odcinku |SK|? Z rysunku to nie wynika

iteRacj@: Odcinek SK jest wysokością trójkąta równoramiennego AKC, prosta w której się zawiera, jest osią symterii trójkąta AKC. Punkt P należy do przekroju sześcianu DBFH, więc jest równoodległy od punktów A i C, z tego wynika, że należy do odcinka SK

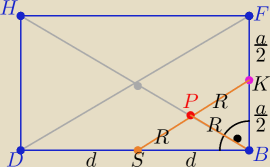
Eta: Pan Jakub za bardzo skomplikował obliczenia Można prościej tak: Na trójkącie prostokątnym KBS można opisać okrąg o średnicy 2R=|SK| |DF|=|BH|=2*|SK|= 4R to |HP|=4R−R= 3R

	|BP|		R
Zatem		=		= 1:3
	|PH|		3R

c.n.w