asymptoty Misiek:

	ex
Asymptoty: y=
	x3

Głównie mi chodzi o as. pozioma czy ukośną. Słownie: e do x przez x do 3 potęgi,

Misiek: Jeszcze jakby ktoś mógł zrobić z tego samego wypukłość i wklesłość, krok po kroku jak sie liczy drugą pochodną. Oraz powiedzieć mi dlaczego wykres dla monotoniczności fukncji leci od góry, skoro po sprowadzeniu do najprostszej postaci mam 2x−x²=0, czyli wspolczynnik przy najwiekszej potedze jest ujemny, czyli powinien iść na dół, a etrapez ma od góry i nie rozumeim dlaczego.

Basia: na mocy reguły de l'Hospitala

	ex		ex		ex		ex
limx→+∞		= limx→+∞		=limx→+∞		= limx→+∞		=
	x3		3x2		6x		6

+∞ czyli asymptoty poziomej prawostronnej nie będzie

	ex
limx→−∞		= 0 bo licznik dąży do 0, a mianownik do −∞
	x3

czyli masz asymptotę poziomą lewostronną y=0

	f(x)		ex
llimx→+∞		=limx→+∞
	x		x4

policz tak jak wyżej stosując regułę de l'Hospitala dostaniesz +∞ czyli nie ma asymptoty ukośnej prawostronnej

	f(x)		ex
limx→−∞		=limx→−∞		= 0
	x		x4

czyli nie ma również asymptoty ukośnej lewostronnej (formalnie jest, ale pokrywa się z poziomą y=0)

Misiek:

	f(x)
A przypadkiem wzór na as. poziomą to nie jest		, bo nie uwzględniłaś tam tego.
	x

Misiek:

	f(x)
Natomiast na as. ukośną f(x) − Ax, gdzie A jest wynikiem z
	x

Misiek: A dobra, przepraszam Cie. Zamotałem. Dziękuje, wszystko sie zgadza. Jeżeli ktoś mógłby jeszcze odpowiedzieć na drugą część czyt.: " Jeszcze jakby ktoś mógł zrobić z tego samego wypukłość i wklesłość, krok po kroku jak sie liczy drugą pochodną. Z tego względu, ze wychodzą mi pierwiastki, a ma ich nie być Oraz powiedzieć mi dlaczego wykres dla monotoniczności fukncji leci od góry, skoro po sprowadzeniu do najprostszej postaci mam 2x−x2=0, czyli wspolczynnik przy najwiekszej potedze jest ujemny, czyli powinien iść na dół, a etrapez ma od góry i nie rozumeim dlaczego."

Basia:

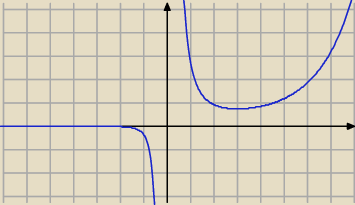
	ex*x3−3x2*ex		x2*ex(x −3)		ex(x−3)
f'(x) =		=		=
	x6		x6		x4

ex
	stale dodatni dla x≠0 czyli miejsce zerowe i znak pochodnej zależą tylko od
x4

wyrażenia y= x−3 x∊(−∞;0) ⇒ f'(x)<0 ⇒ f maleje

	ex
limx→−∞		=0
	x3

	ex
limx→0−		= −∞
	x3

czyli w tym przedziale ona maleje od 0 do −∞ x∊(0;3) ⇒ f'(x)<0 ⇒ f maleje

	ex
limx→0+		= +∞
	x3

	e3
czyli teraz maleje od +∞ do fmin=f(3) =
	27

x∊(3;+∞) ⇒ f'(x)>0 ⇒ f rośnie wykres wygląda jak wyżej

Misiek: Tzn. nie o to mi chodziło. Źle napisałem, przepraszam. Chodziło mi o ekstrema funkcji. Dlaczego ten wykres leci do góry. Wszystko jest mi potrzebne do badania przebiegu zmienności funkcji.

Basia:

	ex(x−3)		x−3
f'(x) =		= ex*
	x4		x4

	x−3		1*x4 − 4x3(x−3)
f"(x) = ex*		+ ex*		=
	x4		x8

	x−3		x4 − 4x4 + 12x3
ex*[		+		] =
	x4		x8

	x−3		−3x4+12x3
ex*[		+		] =
	x4		x8

	x−3		−x3(3x−4)
ex*[		+		=
	x4		x8

	x−3		3x−4
ex*[		−		]=
	x4		x5

	x2−3x−3x+4		x2−6x+4
ex*		=ex*
	x5		x5

no i nie ma zmiłuj, f"(x) ma miejsca zerowe albo gdzieś jest błąd, którego nie widzę

Basia: Rozpisałam Ci wszystkie granice, przeczytaj gdzie i kiedy one są równe +∞, tam wykres "leci" do góry

Misiek: Tzn. Obliczyłaś tylko pochodną pierwszego rzędu. A do wklęsłości trzeba drugiego rzędu i to chodzi, że tam podobno nie ma pierwiastków, a mi wychodzą 2. Natomiast odnośnie ekstrema, to wykres powinien leciec od dołu z tego względu, że współczynnik przy najwyższej potędze jest ujemny, a etrapez ma od góry. Nie wiem w sumie do czego odnosi się post z 17:03

Misiek: Czyli od nowa. 1. Dlaczego wykres jeżeli chodzi o ekstrema funkcji, czyli miejsca zerowe z pierwszej pochodnej leci z prawej strony od góry a nie od dołu. 2. Jeżeli chodzi o wklęsłość i wypukłość, to czy jest możliwość obliczenia tego czyli 2 pochodnej, z tego wzgledu ze wychodza mi 2 pierwiastki, a etrapez nie ma zadnego.

Basia:

	ex		ex
ad.1 bo limx→0+		= +∞ i limx→+∞		= +∞
	x3		x3

ad.2 nie wiem; nie powinno być miejsc zerowych (tak na "oko") a mnie też wyszło, że są; możliwe,że gdzieś jest błąd

Misiek: 1. Ale dlaczego tak Dlaczego tutaj rozpatrujesz granice Z pierwszej pochodnej wychodzą dwa pierwiastki: 0 oraz 2. Pochodna przyrównana do zera ma postać 2x−x²=0. Widzimy, ze najwyzsza potega jest ujemna, czyli wykres zaczynamy z prawje strony od dołu. Gdzie zrobiłem błąd.

Basia: nieprawda

	ex(x−3)
f'(x) =		ma tylko jedno miejsce zerowe x0=3
	x4

granice rozpatruję, bo dla x=0 funkcja nie jest określona czyli trzeba się dowiedzieć jak się zachowuje gdy x→0⁻, a jak gdy x→0⁺

Basia:

	ex
napisałeś f(x) =
	x3

może źle podałeś wzór funkcji, bo pochodna jest zupełnie inna

Misiek: Chyba jeszcze żyje wczorajszą imprezą.

ex
x2

Basia: No to zaczynaj od poczatku x≠0 czyli musisz policzyć

	ex
limx→−∞		= 0
	x2

	ex
limx→0−		= +∞
	x2

	ex
limx→0+		= +∞
	x2

	ex		ex		ex
limx→+∞		= limx→+∞		= limx→+∞		= +∞
	x2		2x		2

	ex*x2 − 2x*ex		ex(x2−2x)		x*ex(x−2)
f'(x) =		=		=
	x4		x4		x4

masz jedno miejsce zerowe x₀ = 2 (0 odpada, bo nie należy do dziedziny) x∊(−∞;0) ⇒ f'(x)>0 ⇒ f rośnie (od 0 do +∞) x∊(0,2) ⇒ f'(x)<0 ⇒ f maleje (od +∞ do minimum) x∊(2;+∞) ⇒ f'(x)>0 ⇒ f rośnie (do +∞)

	e2
fmin = f(2) =
	4

do liczenia drugiej pochodnej wygodniej w pierwszej skrócić x

	x−2
f'(x)= ex*
	x3

	x−2		1*x3 − 3x2(x−2)
f"(x) = ex*		+ ex*		=
	x3		x6

	x−2		x3−3x3+6x2
ex*(		+		)=
	x3		x6

	x−2		−2x3+6x2
ex*(		+		) =
	x3		x6

	x2(−2x+6)
ex*( U{x−2}{x3 +		)=
	x6

	x−2		−2x+6
ex*(		+		) =
	x3		x4

	x(x−2)−2x+6
ex*		=
	x4

ex
	*(x2−4x+6)
x4

y = x²−4x+6 Δ=16−24<0 f"(x) nie ma miejsc zerowych i jest stale dodatnia (oczywiście dla x≠0)

Basia:

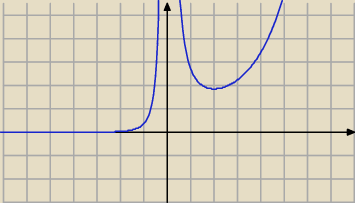
	ex
tak wygąda wykres f(x) =
	x2

Misiek: Nie rozumiem za Chiny tych asymptot.... Ja do obliczania asymptot korzystam z tego: https://zapodaj.net/647ae20401ff1.png.html Asymptota pionowa mi faktycznie wychodzi x=0.

	f(x)
Następnie przechodzę do podpunktu 4. Czyli liczę		− obliczam najpierw x→ −
	x

nieskończoności.

	e do potęgi −nieskończoność
Po podstawieniu mam najpierw [		− z
	−nieskończoność do potęgi 3

teog mi wychodzi niby 0. Później obliczam x → + nieskończoności

	e do potęgi nieskończoność
Po podstawieniu mam [		− z teog mi
	nieskończoność do potęgi 3

wychodzi nieskończoność. Czyli warunek + nieskończoność odpada. Po podstawieniu − nieskończoności do f(x) − ax wychodzi mi nieskończoność.....

Misiek: Teraz zauważyłem znaczek nieskończoności... Eh.

Misiek: Tak, tylko z tym mam problem, narysowałem wszystko i dobrze wyszło. Tylko jakby ktos mi mogl porozpisywac dokladnie te granicy tj. [^∞_∞] etc.

Basia:

	∞
jeżeli masz		stosuj regułę de l'Hospitala
	∞

i masz to już co najmniej dwa razyrozpisane

Misiek: No tak, stosuję ją. Ale widzisz, ze wyniki mam inne niż Ty. Stosuję się do zaleceń schematu, którego zdjęcie podałem.

	f(x)
Czyli najpierw		= A, a nastepnie f(x) − Ax
	x

Basia:

	f(x)		ex
a=limx→+∞		= limx→+∞		= +∞
	x		x3

już Ci to rozpisałam asymptoty prawostronnej ukośnej nie będzie (poziomej też nie, bo to szczególny przypadek ukośnej)

	f(x)		0
a= limx→∞		= limx→∞ U{ex}}{x3} =		= 0
	x		−∞

	ex		0
limx→−∞ (f(x)−0*x) = limx→∞ f(x) = limx→−∞		=		=0
	x2		+∞

czyli masz lewostronną y=0*x+0 czyli y=0 czyli w rzeczywistości poziomą