Stosunek powierzchni bocznej do powierzchni podstawy ostrosłupa prawidłowego czw
Klaudia: Stosunek powierzchni bocznej do powierzchni podstawy ostrosłupa prawidłowego czworokątnego jest
równy k.
b) Wyznacz cosinus kąta zawartego między sąsiednimi krawędziami bocznymi tego ostrosłupa.
Onlicz miarę tego kąta dla k= √3
c) Wykaż, że cosα=−1/k2, gdzie α jest kątem między sąsiednimi ścianami bocznymi tego
ostrosłupa.
31 gru 22:16
Klaudia: Nie mam pomysłu na to zadanie, podpunktu b wgl nie potrafię sobie wyobrazić o który kąt chodzi,
a w c nic mi nie wychodzi z moich wyliczeń. Proszę o pomoc
31 gru 22:17
Mila:
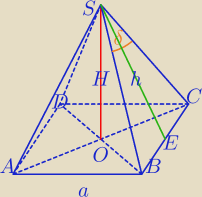
b)
1)
h=0.5 a*k
W ΔSOC:
| | δ | | 0.5a | | 0.5a | | 1 | |
tg |
| = |
| = |
| = |
| |
| | 2 | | h | | 0.5a*k | | k | |
2)
Z jedynki tryg.
| | δ | | δ | | 1 | | k | |
2*sin |
| *cos |
| =2* |
| * |
| |
| | 2 | | 2 | | √1+k2 | | √1+k2 | |
teraz oblicz cosδ
δ=60
0
C) jutro
31 gru 23:41
Mila:
cosδ można prościej, to też jutro.
31 gru 23:57
Mila:
b) cosδ:
b− krawędź boczna
h=0.5 a*k
1) W ΔSEC:
2)
W ΔBCS:
a
2=b
2+b
2−2b
2cosδ
a
2=2b
2−2b
2cosδ
a
2=2b
2*(1−cosδ)
| | 1 | |
a2=2* |
| a2(k2+1)*(1−cosδ) |
| | 4 | |
2=(k
2+1)*(1−cosδ)
k=
√3
δ=60
o
Tak , jak z tangensa.
1 sty 00:11
Klaudia: Okey, dzięki
1 sty 12:01
Mila:
Czy (c) dokończyłaś?
1 sty 19:07
 b)
1)
b)
1)