oblicz pole powierzchni trójkąta PQR kalinka: Dany jest trójkąt ABC o polu powierzchni równym 48 . Punkty KLM są środkami boków trójkątaABC oraz punkty PQR są środkami boków trójkąta KLM . Wykonaj rysunek i oblicz pole powierzchni trójkąta PQR . Uzasadnij odpowiedź.

the foxi: Jedyne co mi przychodzi do głowy to podobieństwo trójkątów. Pokombinuj!

kalinka: własnie to próbowałam, ale musiałabym to udowodnić a nie dokońca wiem jak i w jakiej skali to bdzie

the foxi: Hmmm, weźmy trójkąt KLM i nowopowstały trójkąt AKM. Miara kąta KAM=mierze kąta BAC. Tak samo kąty AKM i KMA − odpowiednie miary jak w kątach ABC i BCA. Więc są pdoobne. Długości każdego boku są krótsze o połowę, zatem k=0.5 Podobna sytuacja powinna mieć miejsce w trójkącie PQR, ale nie mam nawet jak tego rozrysować obecnie Pamiętaj związek między polem a skalą podobieństwa k = p=k²

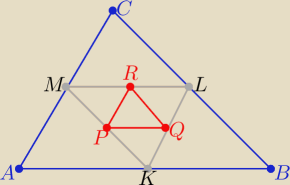
Eta: P(ABC)=48

	48
ΔABC∼ ΔKLM w skali k=2 ⇒ P(KLM)=		= 12
	k2

	12
ΔKLM ∼ ΔPQR w skali p=2 ⇒ P(PQR)=		= 3
	p2

P(PQR)=3 [j²] =======

kalinka: dziękuję eta lecz potrzebuje mieć niestety napisane dokładnie dlaczego są podobe ( z jakiej cechy), to juz zrobiłam ale początka nie mam