Punkt na powierzchni - procentowy współczynnik odległości
Zakłopotany:

Mając dany punkt P(x, y) oraz 4 punkty (A, B, C, D) składające się na powierzchnie czworoboku
(patrz rysunek).
Oblicz odległość procentową punktu między bokami AB oraz CD, gdzie
0% − punkt leży na boku AB,
100% − punkt leży na boku CD.
Próbowałem stworzyć układ z 5 równaniami ale zmiennych jest tak dużo (bo nie podano wartości
liczbowych), że w połowie rozwiązywania równania zajmuje ono pól strony A4 i już na horyzoncie
widać równanie kwadratowe...
Jakiś pomysł?
btw. Bok AD oraz BC nie muszą być równoległe − zadanie ma być rozwiązane dla dowolnego
czworoboku.
Zakłopotany:
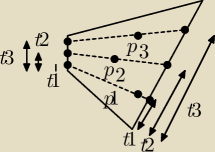
Wybacz, źle narysowałem rysunek.
Ten jest dal przykładowych 3 punktów, dla szukanych wartości t1, t2, t3.
 Mając dany punkt P(x, y) oraz 4 punkty (A, B, C, D) składające się na powierzchnie czworoboku
(patrz rysunek).
Oblicz odległość procentową punktu między bokami AB oraz CD, gdzie
0% − punkt leży na boku AB,
100% − punkt leży na boku CD.
Próbowałem stworzyć układ z 5 równaniami ale zmiennych jest tak dużo (bo nie podano wartości
liczbowych), że w połowie rozwiązywania równania zajmuje ono pól strony A4 i już na horyzoncie
widać równanie kwadratowe...
Jakiś pomysł?
btw. Bok AD oraz BC nie muszą być równoległe − zadanie ma być rozwiązane dla dowolnego
czworoboku.
Mając dany punkt P(x, y) oraz 4 punkty (A, B, C, D) składające się na powierzchnie czworoboku
(patrz rysunek).
Oblicz odległość procentową punktu między bokami AB oraz CD, gdzie
0% − punkt leży na boku AB,
100% − punkt leży na boku CD.
Próbowałem stworzyć układ z 5 równaniami ale zmiennych jest tak dużo (bo nie podano wartości
liczbowych), że w połowie rozwiązywania równania zajmuje ono pól strony A4 i już na horyzoncie
widać równanie kwadratowe...
Jakiś pomysł?
btw. Bok AD oraz BC nie muszą być równoległe − zadanie ma być rozwiązane dla dowolnego
czworoboku.
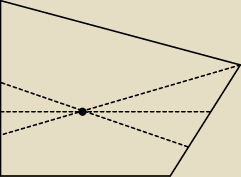 A ta linia przerywana ma mieć jakieś konkretniej określone położenie czy może sobie być "jak
chce"?
Rysunek pokazuje o co mi chodzi.
A ta linia przerywana ma mieć jakieś konkretniej określone położenie czy może sobie być "jak
chce"?
Rysunek pokazuje o co mi chodzi.
 Wybacz, źle narysowałem rysunek.
Ten jest dal przykładowych 3 punktów, dla szukanych wartości t1, t2, t3.
Wybacz, źle narysowałem rysunek.
Ten jest dal przykładowych 3 punktów, dla szukanych wartości t1, t2, t3.