:( Filip: W okrąg o promieniu ⁵₂ wpisano ośmiokąt A₁A₂A₃A₄A₅A₆A₇A₈ tak, że czworokąt A₁A₃A₅A₇ jest prostokątem o polu równym 12. Jakie jest największe pole takiego ośmiokąta?

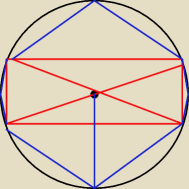
Basia: przekatna c=2r = 5 a²+b²=25 a*b = 12

	12
b =
	a

	144
a2+		= 25
	a2

a⁴ + 144 = 25a² a⁴−25a²+144 = 0 Δ=625−576 = 49 √Δ=7

	25−7
a2 =		= 9 czyli a=3 i b=4
	2

lub

	25+7
a2 =		= 16 czyli a=4 i b=3
	2

czyli boki prostokąta mają długości a=4 i b=3 (lub na odwrót, ale to wszystko jedno) do pola prostokąta trzeba dodać pola tych czterech trójkątów największe te pola będą gdy wysokości są największe

	5		3		5		4		1
czyli wtedy gdy h1 =		−		= 1 a h2=		−		=
	2		2		2		2		2

	1		1		1
P = 12+2*		*4*1+2*		*3*
	2		2		2

dokończ obliczenia