Zbadaj czy istnieje tak wartosc parametrów k,m dla których funkcja f jest różnic franek: Zbadaj czy istnieje tak wartosc parametrów k,m dla których funkcja f jest różniczkowalna w zbiroze R. Wyznacz f'

	⎧	mx2+(k+1)x jeśli x<−1
f(x)=	⎩	kx2−3mx, jeśli x≥−1

Jerzy: To funkcja kwadratowa, więc wystarczy, aby była ciągła w x = −1

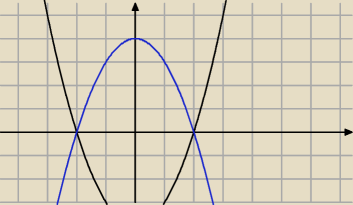
Basia: jesteś pewny? a jak będzie takie coś jak na rysunku i zdefiniujemy f(x) = −x²+4 dla x≤2 f(x) = x²−4 dla x>2 ciagla będzie, ale czy różniczkowalna? nie liczyłam, ale tam jest ostrze więc raczej różniczkowalna nie bedzie Oczywiście najpierw trzeba okreslić dla jakich parametrów ta funkcja z zadania jest ciągla w −1 bo jeżeli nie jest ciągła to nie jest różniczkowalna Jeżeli okaże się, że da to ten sam wzór to koniec, ale jeżeli nie to niezupełnie

Basia: lim_x→−1⁺f(x) = f(−1) = k+3m lim_x→−1⁻f(x) = m−k−1 musi być k+3m = m−k−1 2m + 2k = −1

	−1−2k		1
m =		= −k−
	2		2

czyli ta funkcja będzie ciągła dla każdej pary (m,k) spełniającej podany warunek niewiele nam to daje (na razie, bo bedzie potrzebne) jeżeli funkcja ma być różniczkowalna to granica pochodnej lewostronnej w −1 = pochodna prawostronna w −1 f'_l = 2mx+k+1 f'_p = 2kx−3m f'_p(−1) = −2k−3m lim_x→−1 f'_l = −2m+k+1 i teraz układ równań z ciągłości 2m+2k = −1 z różniczkowalności −2k+3m=−2m+k+1 5m−3k= 1 2m+2k=−1 5m−3k=1 6m+6k=−3 10m−6k=2 −−−−−−−−−−−−− 16m = −1

	1
m = −
	16

2
	+2k = −1
16

1
	+2k = −1
8

	9
2k = −
	8

	9
k = −
	16

o ile gdzieś się nie pomylilam w rachunkach