| x2 | ||
2): | ≤y≤2√x | |
| 2 |
| x2 | 2 | |||
3): | ≤y≤ | |||
| 2 | √x |
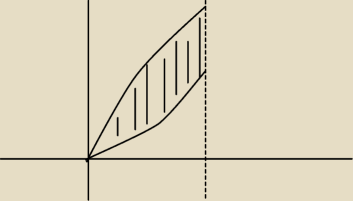 Sorki, ale nie potrafię w tym rysować za dobrze.
To tak:
Skorzystamy z zależności na objętość bryły obrotowej względem osi OX za pomocą całki:
Wzór:
V=π ∫ab [f(x)]2 dx
gdzie V−objętość bryły powstałej z obrotu figury G wogół osi OX
U Ciebie:
1) oblicz objętość bryły G1 gdzie a=0, b=1, f(x)=2√x
2) oblicz objętość bryły G2 gdzie a=0, b=1, f(x)=x2
3) odejmij objętość bryły G1 objętość bryły G2 i otrzymasz wynik
Powodzenia!
Sorki, ale nie potrafię w tym rysować za dobrze.
To tak:
Skorzystamy z zależności na objętość bryły obrotowej względem osi OX za pomocą całki:
Wzór:
V=π ∫ab [f(x)]2 dx
gdzie V−objętość bryły powstałej z obrotu figury G wogół osi OX
U Ciebie:
1) oblicz objętość bryły G1 gdzie a=0, b=1, f(x)=2√x
2) oblicz objętość bryły G2 gdzie a=0, b=1, f(x)=x2
3) odejmij objętość bryły G1 objętość bryły G2 i otrzymasz wynik
Powodzenia!