Przebieg zmienności funkcji Fanabela: Witam, mam pytanie dotyczące przebiegu zmienności funkcji, a mianowicie badam taką funkcje: f(x)=(x+1)³/(5(x−1)²) Obliczyłam dziedzinę, asymptoty, pochodne, przecięcia funkcji z OX i OY. Z obliczeń wynika, że między innymi f'=((x+1)²(x−1)(x−5))/(5(x−1)⁴) −> f↑ x należy do (5,+∞); f↓ x należy do (−∞,−1),(−1,1),(1,5) f''=(x+1)24/(5(x−1)⁴) −> wypukła x należy do (−1,+∞), wklęsła x należy do (−∞,−1) Problem polega na tym, że gdy sprawdzam wykres funkcji w programie do rysowania wykresów to tam gdzie według mnie powinna maleć rośnie, a tam gdzie rosnąć maleje. Wszystko inne się zgadza. Nie wiem gdzie w moim rozumowaniu jest błąd. Proszę o pomoc

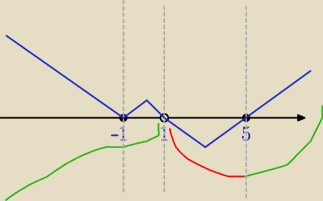
ford: myślę że źle analizujesz wykres pochodnej f' załączam niebieski prawidłowy wykres pochodnej dla x=1 f(x) nie jest określona więc liczymy granice lim_x→1⁻ f(x) i lim_x→1⁺ f(x) i obie będą równe +∞ na podstawie niebieskiego wykresu pochodnej f'(x) oraz granic lim_x→1⁻ f(x) i lim_x→1⁺ f(x) mogę narysować zielono−czerwony wykres f(x) zgodnie z zasadą: pochodna dodatnia (niebieski wykres nad osią x − wtedy f(x) rosnąca) pochodna ujemna (niebieski wykres pod osią x − wtedy f(x) malejąca)

Fanabela: Dziękuję! Już wszystko jasne (trywialny błąd) Nie uwzględniłam 1 z mianownika i dlatego obliczenia się nie zgadzały. Mam jeszcze pytania dotyczące badania przebiegu funkcji: f(x)=√x³/(x+3) ponieważ f'=(√x(2x+9))/(2(x+3)^3/2) punkty podejrzane o bycie ekstremum to x=−⁹₂ v x=0 i nie wiem co należy zrobić z tymi punktami, bo mimo że wpadają do dziedziny funkcji ((−∞,−3)u<0,+∞)) to nie należą do dziedziny f'. f''=27/(4√x(x+3)^5/2) i nie wiem jak z takiej funkcji wyznaczyć możliwe punkty przegięcia.

iteRacj@: pierwsza pochodna

	x2*(2x+9)
f'=
	x3   2√ *(x+3)2   x+3

	x2*(x+4,5)
f'=
	x3   √ *(x+3)2   x+3

dziedzina funkcji pochodnej: D_f' = (−∞,−3)∪(0,+∞) zmiana znaku pochodnej dla x=−4,5, jest to minimum lokalne druga pochodna

	27x
f'=
	x3   4√ *(x+3)3   x+3

dziedzina dla drugiej pochodnej: D_f" = (−∞,−3)∪(0,+∞) druga pochodna dodatnia w całej dziedzinie, brak punktów przegięcia

	x3
*pod pierwiastkiem jest wszędzie iloraz
	x+3