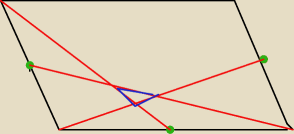
 W równoległoboku środki trzech boków połączono z odpowiednimi wierchołkami tak jak na rysunku.
Oblicz stosunek pola równoległoboku do pola otrzymanego trójkata (niebieski).
W równoległoboku środki trzech boków połączono z odpowiednimi wierchołkami tak jak na rysunku.
Oblicz stosunek pola równoległoboku do pola otrzymanego trójkata (niebieski).

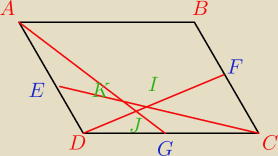 jc, a możesz to zrobić za pomocą reguły dźwigni?
ktoś mi to pokazywał, ale zapomniałem jak to się robi
(można za pomocą tego poznać stosunek niektórych odcinków do siebie)
jc, a możesz to zrobić za pomocą reguły dźwigni?
ktoś mi to pokazywał, ale zapomniałem jak to się robi
(można za pomocą tego poznać stosunek niektórych odcinków do siebie)
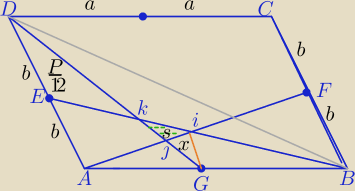 PABCD=P
PABCD=P
| 1 | ||
PΔABD= | P | |
| 2 |
| 1 | 1 | |||
PΔDEK=PΔBGK= | PΔABD= | P | ||
| 6 | 12 |
| 1 | ||
|GI|= | b | |
| 2 |
| 1 | ||
ΔKGI∼ΔDEK w skali k= | ⇔ | |
| 2 |
| 1 | 1 | 1 | ||||
PΔKGI= | *PΔDEK= | P⇔s+x= | P | |||
| 4 | 48 | 48 |
| s | KJ | ||
= | |||
| x | JG |
| 1 | ||
|KG|= | d | |
| 3 |
| 1 | ||
Zatem |GJ|= | d | |
| 5 |
| 1 | 1 | 2 | ||||
|KJ|= | d− | d= | d | |||
| 3 | 5 | 15 |
| s | 2d | d | 2 | ||||
= | : | = | ⇔2x=3s | ||||
| x | 15 | 5 | 3 |
| 3 | 3 | 1 | ||||
x= | s ⇔s+ | s= | P | |||
| 2 | 2 | 48 |
| 5 | 1 | 1 | |||
s= | P ⇔s= | P | |||
| 2 | 48 | 120 |
| P | |
=120 | |
| s |
 Nie podzieliłem wyniku przez 2. Pole trójkąta = pole odpowiedniego równoległoboku / 2.
Gdzieś mi ta dwójka umknęła.
Wydaje mi się, że odpowiedni rysunek może dać odpowiedź prawie bez rachunku.
Mamy wybór: bezmyślne rozwiązanie (np. moje algebraiczne) czy krótkie pomysłowe
Na sprawdzianie stawiałbym na schemat, w domu na rozmyślania.
Nie podzieliłem wyniku przez 2. Pole trójkąta = pole odpowiedniego równoległoboku / 2.
Gdzieś mi ta dwójka umknęła.
Wydaje mi się, że odpowiedni rysunek może dać odpowiedź prawie bez rachunku.
Mamy wybór: bezmyślne rozwiązanie (np. moje algebraiczne) czy krótkie pomysłowe
Na sprawdzianie stawiałbym na schemat, w domu na rozmyślania.
| 1 | ||
Dziękuję za odpowiedź, tak myślałam, że brakuje | . | |
| 2 |
 Ciekawe o co zapyta uczennica? (chyba wiem)
Ciekawe o co zapyta uczennica? (chyba wiem)