zad pytajnik:

	1
Dane jest równanie |		− 4|=p z parametrem p . Wyznacz liczbę rozwiązań tego
	2x

równania w zależności od parametru p

pytajnik: czy to bedzie I roz dla x∊(4;∞) ?

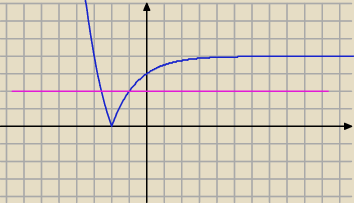
Jerzy: Różowa: y = p

Jerzy: Tak, w tym przedziale bedzie tylko jedno rozwiązanie.

pytajnik: II roz dla x∊(−∞;4)

pytajnik: dobra zapomniałam o wartosći bezwglednej to bedzie x∊(0;4)

Basia: dla p<0 nie ma rozwiązań

	1
dla p=0 masz		−4=0 rozwiąż jest jedno rozwiązanie
	2x

	1		1
dla p>0 masz		−4 = p lub		−4 = −p
	2x		2x

1
	=p+4 na pewno ma rozwiązanie dla dowolnego p>0
2x

1
	=4−p niekoniecznie
2x

dla 4−p≤0 nie ma rozwiązania, dla 4−p>0 jest ostatecnie; dla p<0 nie ma rozwiązań dla p=0 i p≥4 jedno rozwiązanie dla p∊(0;4) dwa a w ogóle to najłatwiej rozwiązać to graficznie

Jerzy: Nie. p ∊ (0,4) − dwa p = 0 lub p ∊ [0,+∞) − jedno p < 0 − brak

Jerzy: @Basia dla p = 0 lub p ≥ 4

Basia: (0;4)⊂<0;+∞) coś nie gra

Basia: dla p=0 i dla wszystkich p≥4 (tak to trzeba przeczytać)

Jerzy: Nie ma p = 0 i p ≥ 4

Basia: to nie jest koniunkcja zdań dotyczących p oczywiście, że p=0 ∧ p≥4 jest sprzecznoscia nie jest sprzecznością koniunkcja dla p=0 równanie ma jedno rozwiązanie i dla p≥4 równanie ma jedno rozwiązanie