Wyznaczyć rzut punktu Sheller: Wyznaczyć rzut punktu P(6,36,−38) na prostą l: ^x−20₋₇ = ^y−13₋₆ = ^z−6₋₇ a także równanie płaszczyzny przechodzącej przez punkt P i prostopadłej do prostej l

jc: To punkt przecięcia prostej (x,y,z)=(20,13,6)−t(7,6,7) z płaszczyzną 7(x−6)+6(y−36)+7(z+38)=0.

Sheller: Nie bardzo rozumiem to zadanie, ale kiedy chce wyznaczyć punkt P' z tego układu równań:

⎧	7x+6y+7z+6=0
⎜	x=−7t+20
⎨	y=−6t+13
⎩	z=−7t+6

to po wstawieniu równania parametrycznego prostej do równania płaszczyzny to "t" wychodzi mi jako dziwny ułamek. Gdzie robię błąd?

Sheller: Udało mi się chyba rozwiązać zadanie. Mógłby ktoś sprawdzić czy jest poprawnie?

⎧	7x+6y+7z+6=0
⎜	x=20−7t
⎨	y=13−6t
⎩	z=6−7t

7*(20−7t)+6*(13−6t)+7*(6−7t)+8=0 −134t=268 t=−2 P'=[34,25,20]

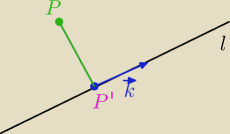
Mila: wektor PP' ma być prostopadły do k^→=[−7,−6,−7] Błędnie obliczyłeś t, t=2 II sposób P'∊l⇔P'=(20−7t,13−6t,6−7t) rzut punktu P na prostą l PP'^→=[14−7t,−23−6t44−7t] k^→o PP'→=0⇔ −7*(14−7t)−6*(−23−6t)−7*(44−7t)=0 t=2 P'=(6,1,−8) Spr. P(6,36,−38) PP'=[6−6,1−35,8−(−38)]=[0,−35,30] [0,−35,30] o [−7,−6,−7]=210−210=0 Równanie płaszczyzny jak u Jc n^→=k^→ [−7,−6,−7] || [7,6,7] P∊π 7*(x−6)+6*(y−36)+7*(z+38)=0 π: 7x+6y+7z+8=0

Sheller: Bardzo dziękuję.

Mila: