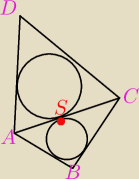
Planimetria Satan: Dany jest taki czworokąt wypukły ABCD, że okręgi wpisane w ΔABC i ΔADC są styczne. Wykaż, że w czworokąt ABCD można wpisać okrąg. Więc tak: Najpierw ΔABC:

	|AB|		|AS|
Z twierdzenia o dwusiecznej kąta wewnętrznego w Δ:		=
	|BC|		|SC|

Teraz ΔADC:

	|AD|		|AS|
Z twierdzenia o dwusiecznej kąta wewnętrznego w Δ:		=
	|DC		|SC|

	|AB|		|AS|		|AD|		|AB|		|AD|
Więc mam:		=		=		→		=		= k
	|BC|		|SC|		|DC		|BC|		|DC

W takim razie ΔABC ~ ΔADC. W takim razie |∡BAC| = |∡DAC| ∧ |∡BCA| = |∡DCA| ∧ |∡ABC| = |∡ADC|. No i teraz skoro kąty: |∡BAC| = |∡DAC| ∧ |∡BCA| = |∡DCA| są równe, to odcinek |AC| jest sieczną kątów |∡BAD| i |∡BCD|. I teraz mam małą zagwozdkę. Czy tworzyć ΔBAC i ΔBCD poprzez dorysowanie odcinka |BD| i w analogiczny sposób udowodnić, że ΔBAD ~ ΔBCD, a potem, że |DB| jest sieczną dwóch kątów jednocześnie i na podstawie twierdzenia, które brzmi: w czworokąt wypukły można wpisać okrąg wtedy i tylko wtedy, gdy wszystkie dwusieczne kątów tego czworokąta przetną się w jednym punkcie. Czy może macie inny sposób na to zadanie, a mój tok myślenia jest błędny? Wszelkie uwagi, naprostowania i odpowiedzi mile widziane

g: Twierdzenie o dwusiecznej nie ma tu zastosowania bo punkt S niekoniecznie leży na dwusiecznej.

Satan: Otóż to właśnie dowiodłem, tak myślę. Okręgi są styczne zewnętrznie, czyli istnieje styczna przechodząca przez ten jeden punkt − w moim wypadku oznaczyłem go jako S. Twierdzenie o dwusiecznej zastosowałem dla dwusiecznych kątów: |∡ABC| oraz |∡ADC|, gdyż środek okręgu wpisanego w trójkąt leży na przecięciu się dwusiecznych trójkąta Dopiero po dowodzie, że |AC| dzieli kąty przy wierzchołkach A i C na dwa równe kąty stwierdzam, że styczna |AC| jest jednocześnie dwusieczną. W takim wypadku prowadząc nowy odcinek |BD|, który będzie nową styczną nowych okręgów, w powstałych trójkątach będą one miały wspólną sieczną |AC| No, chyba, że się grubo mylę

===: Jeden z moich Starszych BELFRÓW (niestety już świętej pamięci} zwykł powiadać: − jesli krocząc do przodu natrafiłeś na ścianę masz w sumie dwa wyjscia: albo walić z główki w tą ścianę albo zrobić krok do tyłu i popatrzeć czy gdzies z boku nie ma otwartych drzwi. Odpowiedz sobie na pytanie kiedy w czworokąt można wpisać okrąg.

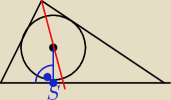
g: Środek okręgu leży na dwusiecznej, ale punkt S to nie jest środek okręgu.

Satan: To wiem, też się zastanawiałem. Tylko najpierw chciałem wykorzystać fakt, że okrąg można wpisać w czworokąt, gdy dwusieczne jego kątów przecinają się w jednym punkcie. Chciałem ominąć to, że pary przeciwległych boków muszą być równe co do sumy, bo to jest równoznaczne (chyba) z dwusiecznymi. Jeszcze trocję pracy przede mną. Ale − jeszcze nad tym pomyślę, to pewne!

Satan: @g, owszem, to tylko punkt, gdzie okręgi są styczne. Miałem na myśli, że w zasadzie jest on mało ważny przy wyznaczaniu okręgu wpisanego w czworokąt. Już nie rysowałem drugiego odcinka i punktu przecięcia

===: Patrz na poszczególne odcinki boków i zauważ, ze powtarzaja się one w każdej z par

Satan: O raaaany... Już wiem! Faktycznie, można walić głową w ścianę Zaraz zrobię, tylko zjem

===: i jak widzisz szkoda główki

Satan: Oj bardzo szkoda, dziękuję Wam za wszelkie uwagi i komentarze

===: