pomocy. Suma długości i wysokości podstawy. Belek: Suma długości wysokości podstawy i wysokości ściany bocznej ostrosłupa prawidłowego trójkątnego jest równa 2. Wyznacz długość krawędzi podstawy tego ostrosłupa, dla której ma on największe pole powierzchni całkowitej.

Bogdan:

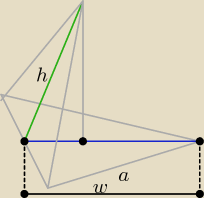
	√3
w =		a,
	2

	√3
h + w = 2 ⇒ h = 2 −		a
	2

	√3		1
P =		a2 + 3*		ah → max
	4		2

	√3		1		√3		√3		3√3
P =		a2 + 3*		a*(2 −		a) =		a2 + 3a −		a2
	4		2		2		4		4

	√3
P = −		a2 + 3a
	2

	√3
Otrzymaliśmy funkcję kwadratową P(a) = −		a2 + 3a posiadającą maksimum
	2

	−3
dla a =		= √3
	−√3   2 *   2

	−b
Skorzystaliśmy tu z wzoru na odciętą wierzchołka paraboli xw =
	2a