 Zad 2.
Zrobiłbym to tak (nie daję 100% poprawności)
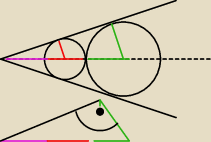
Fioletowy kolor, odległość = x
Czerwony kolor, odległość = 2r
Zielony kolor, odległość = 3r
Z twierdzenia Talesa:
Zad 2.
Zrobiłbym to tak (nie daję 100% poprawności)
Fioletowy kolor, odległość = x
Czerwony kolor, odległość = 2r
Zielony kolor, odległość = 3r
Z twierdzenia Talesa:
| x+2r | x+2r+5r | ||
= | |||
| 2r | 3r |
| 3r | 1 | √6 | ||||
tgα = | = | = | ||||
| 6√6r | 2√6 | 12 |
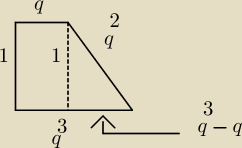 Zad.1
Tutaj mogą być chyba dwa przypadki:
1) tak jak na rysunku bok = 1 jest wysokością
2) bok = 1 jest górną podstawą trapezu (na rysunku zamiast q)
Skorzystaj z tw.pitagorasa (do rysunku)
12+(q3−q)2=(q2)2 oraz założenie, że q>1
mi wyszło q=√1+√52, ale sam sobie to policz i policz 2 przypadek
Zad.1
Tutaj mogą być chyba dwa przypadki:
1) tak jak na rysunku bok = 1 jest wysokością
2) bok = 1 jest górną podstawą trapezu (na rysunku zamiast q)
Skorzystaj z tw.pitagorasa (do rysunku)
12+(q3−q)2=(q2)2 oraz założenie, że q>1
mi wyszło q=√1+√52, ale sam sobie to policz i policz 2 przypadek
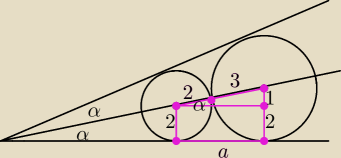
| 1 | √6 | |||
2) a = √25 − 1 = 2√6, tgα = | = | |||
| 2√6 | 12 |