Badanie przebiegu zmienności funkcji Student_1_rok: Cześć, czy umiałby ktoś pomóc z tymi dwoma przykładami z badania przebiegu zmienności funkcji? Pilne 1. y = 1/2 x² + 1/x 2. y = x²+1/x²−4 Głównie zależy mi na dziedzinie, asymptotach, monotoniczności, minimum / maximum, wklęsłość, wypukłość oraz punkty przegięcia.

Bogdan: ho ho , to huk roboty, nawet dziedziny nie potrafisz wyznaczyć?

the foxi:

	1		1		1		2x		2x+1
1. y=		+		=		+		=
	2x2		x		2x2		2x2		2x2

Dziedzina: ℛ\{0} Asymptoty:

	2x+1
pozioma: lim (x→+∞)		=0, czyli y=0
	2x2

pionowa: x=0

	2x+1		2(2x2)−4x(2x+1)		4x2−8x2−4x		−4x2−4x
y'=(		)'=		=		=
	2x2		4x4		4x4		4x2

Przedziały monotoniczności: y'>0 ⇔ 4x²(−4x²−4x)>0 ⇒ −16x³(x²+1)>0 ⇒ x<0 y'<0 ⇔ 4x²(−4x²−4x)<0 ⇒ −16x³(x²+1)<0 ⇒ x>0 Ekstrema:

−4x2−4x
	=0 ⇔ −4x2−4x=0 ⇒ x=0∉D ⋁ x=−1∊D ← minimum
4x2

	−4x2−4x		(−8x−4)(4x2)−8x(−4x2−4x)
y''=(		)'=		=
	4x2		16x4

	−32x3−16x2+32x3+32x2		16x2
=		=
	16x4		16x4

Funkcja wypukła:

	16x2
y''>0 ⇔		>0 ⇒ 16x2*16x4>0 ⇒ x∊ℛ\{0} (czyli w całej dziedzinie)
	16x4

Funkcja wklęsła:

	16x2
y''<0 ⇔		<0 ⇒ 16x2*16x4<0 ⇒ x=0∉D
	16x4

Punkt przegięcia:

	16x2
y''0 ⇔		=0 ⇒ x=0∉D
	16x4

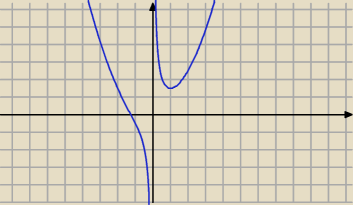
Jack: oj student student... studenty maja teraz wolne...

	1		1
1. y =		x2 +
	2		x

D = R \ {0} przeciecia z osiami: dla y = 0

	1		1		1		1
0 =		x2 +		−−> 0 =		x3 + 1 −−>		x3 = − 1
	2		x		2		2

x = − ³√2 zatem mamy punkt (−³√2,0) Granice w punktach nienalezacych do dziedziny (czyli x=0):

	1		1
lim (		x2 +		) = − ∞ −−>wniosek: asymptota pionowa lewostronna x=0
	2		x

x−>0⁻

	1		1
lim (		x2 +		) = ∞ −−>wniosek: asymptota pionowa prawostronna x=0
	2		x

x−>0⁺ wniosek : granica obustronna x=0 (wystarczy ten wniosek napisac, tych dwoch powyzej nie trza) granice w nieskonczonosciach:

	1		1
lim (		x2+		) = ∞
	2		x

x−>−∞

	1		1
lim (		x2+		) = ∞
	2		x

x−>∞ wniosek: brak asymptoty poziomej. Sprawdzmy jeszcze asymptote ukosna. Asymptota ukosna okreslona jest wzorem y = ax + b gdzie

	f(x)
a = lim
	x

b = lim (f(x) − ax) przy + − nieskonczonosciach obie granice. Zatem

	1		1
a = lim (		x+		) = ± ∞
	2		x2

x−>±∞ Skoro 'a' nie jest okreslona konkretna liczba...to wniosek: brak asymptoty ukosnej Pierwsza pochodna (ekstrema + monotonicznosc):

	1		1		1
f'(x) = (		x2+		)' = x −
	2		x		x2

	1
f'(x) = 0 −−> x −		= 0 −−> x3 = 1 −−> x = 1
	x2

	1		1		3
zatem ekstremum lokalne x=1, ktorego wartosc wynosi: f(1) =		+		=
	2		1		2

f'(x) > 0

	1
x −		> 0 /*x2 (moge pomnozyc bo x2 jest nieujemne)
	x2

x³ − 1 > 0 (x−1)(x²+x+1) > 0 x > 1 wniosek: dla x ∊ (1;∞) f'(x)>0 funkcja rosnie f'(x) < 0

	1
x −		< 0 /*x2 (moge pomnozyc bo x2 jest nieujemne)
	x2

x³ − 1 < 0 (x−1)(x²+x+1) < 0 x < 1 wniosek: dla x ∊ (−∞;0) U (0;1) f'(x)<0 funkcja maleje. druga pochodna (punkty przegiecia + wkleslosc/wypuklosc)

	1		2
f''(x) = (x −		)' = 1 +
	x2		x3

	2
f''(x) = 0 −−> 1 +		= 0 −−> x3 = − 2 −−−> x = 3√−2 = −3√2
	x3

zatem mamy punkt przegiecia dla x = −³√2 f''(x) > 0

	2
1 +		> 0
	x3

x3+2
	> 0
x3

x³(x³+2) > 0 x ∊ (−∞;−³√2) U (0;∞) wniosek : dla x ∊ (−∞;−³√2) U (0;∞) f''(x) > 0 funkcja jest wypukla czyli ∪ f''(x) < 0

	2
1 +		< 0
	x3

x3+2
	< 0
x3

x³(x³+2) < 0 x ∊ (−³√2 ; 0) wniosek : dla x ∊ (−³√2 ; 0) f''(x) < 0 funkcja jest wklesla czyli ∩ Teraz tylko tabelka i zawrzec te wszystkie informacje

the foxi: ...i teraz pytanie, o którą funkcję chodziło.

Jack:

	1
na 99% 1/2x2 oznacza		x2...
	2

the foxi:

	1		1
Hmm, faktycznie.		+		wygląda zbyt "prosto".: >
	2x2		x

Jack: jak cos ja z drugiego od razu rezygnuje,... nie chce mi sie

kochanus_niepospolitus: Ja w ogóle nie wiem co po robicie mu gotowca skoro ten koleś nawet się słowem nie odezwał od wpisania zadania Baaa ... nawet dziedziny nie potrafi zrobić.

Student_1_rok: Skoro komuś tak usilnie zależy aby mnie wywołać, to jestem, ten co czeka na gotowca, a więc tak: rzeczywiście nie potrzebnie wpisałem, że zależy mi na dziedzinie ponieważ to wyznaczę ale w reszcie miewałem problemy i poprosiłem o całość, a i przepraszam, że zapisałem tak tą funkcję, że był problem z odczytaniem jaką ona ma formę czy 1/2 x² czy 1/2x² . Dziękuję za pomoc. A ,,kochanus_niepospolitus" to, że ktoś nie odezwał się od razu po wpisach nie znaczy, że ma wyje**** widocznie robił coś innego, może dalej sam próbował zrobić ten przykład? oh idiotus zawistus.

Jack: akurat kochanus to Ty szanuj ;x

Student_1_rok: Przyjąłem postawę taką jak ,,kochanus". A Panu dziękuję za pomoc!

Qulka: wolfram alpha policzy dziedzinę granice pochodne extremum i całki przy okazji no i namaluje ...więc będzie miał gotowca od ręki np .: http://www.wolframalpha.com/input/?i=(x%5E2%2B1)%2F(x%5E2%E2%88%924)