Wykaż, że miara kąta wypukłego SCB jest równa 45 . karolina: Dany jest trójkąt prostokątny ABC , w którym kąt ACBjest prosty. Na przeciwprostokątnej tego trójkąta zbudowano na zewnątrz trójkąta kwadrat o boku długości AB . Punkt S jest środkiem symetrii tego kwadratu. Wykaż, że miara kąta wypukłego SCB jest równa 45 . skorzystaj z instrukcji: Wykonanie rysunku i zaznaczenie kąta SCB Zauważenie i zapisanie wniosku, że na czworokącie ASBC można opisać okrąg Uzasadnienie miary kąta SBC z wykorzystaniem twierdzenia o kątach wpisanych

karolina: ip

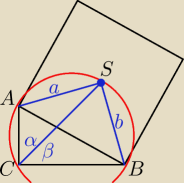
g: α=β ponieważ a=b. skoro α+β=90, to α=45

karolina: g mógł bys to bardziej opisać?

karolina: pomoże ktoś?

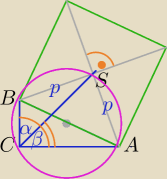
Mila: 1) Punkt przecięcia przekątnych kwadratu jest środkiem symetrii tego kwadratu Przekątne są prostopadłe , równe i dzielą się na połowy⇔ ∡ACB=∡ASB=90^o 2) Sumy kątów przeciwległych w czworokącie ASBC mają po 180^o⇔ na tym czworokącie można opisać okrąg 3) ∡α,∡β− kąty wpisane w okrąg oparte na równych cięciwach BS i AS⇔ ∡α=∡β i α+β=90⇔ |∡SCB|=45^o