Znajdz przedziały monotoniczności oraz ekstrema mat1510: Mam pytanie odnośnie tego przykładu:

	x+1
f(x)= ln
	x−1

1. D= (−∞;−1)U(1;∞)

	x+1		−2
2, pochodna : [ln		]'=
	x−1		(x−1)2

3, f'(x)=0

−2
	= 0 / *(x−1)2
(x−1)2

−2=0 czy to oznacza ze nie ma żadnych przedziałów monotoniczności i ekstremów , czy coś żle napisałem

piotr: funkcja jest malejąca w całej dziedzinie

piotr: nie ma ekstremów

Jerzy: To nieprawda. Funkcja jest malejąca w przedziałach.

piotr: Jerzy, co jest nieprawdą?

Jack:

	x−1		x−1 − (x+1)		x−1		−2		−2
f'(x) =		*		=		*		=
	x+1		(x−1)2		x+1		(x−1)2		(x−1)(x+1)

f'(x) = 0

−2
	= 0
(x−1)(x+1)

−2 = 0 wniosek: brak ekstremow lokalnych teraz przedzialy monotonicznosci: funkcja rosnie, gdy f'(x) > 0

−2
	> 0
(x−1)(x+1)

−2(x−1)(x+1) > 0 x ∊ (−1;1) jednakze ten przedzial nie nalezy do dziedziny. teraz kiedy maleje f'(x) < 0

−2
	< 0
(x−1)(x+1)

−2(x−1)(x+1) < 0 (x−1)(x+1) > 0 x ∊ (−∞;−1) U (1;∞) Zatem wniosek: f ' (x) < 0 dla x ∊ (−∞;−1) U (1;∞), funkcja maleje Czyli funkcja maleje w calej swojej dziedzinie.

Jerzy: Nie macie koledzy racji. Ta funkcja maleje w przedziałach, ale nie maleje w całej dziedzinie. To bzdura.

Jack: formalnie mowiac ok, zgodze sie ze maleje w przedzialach

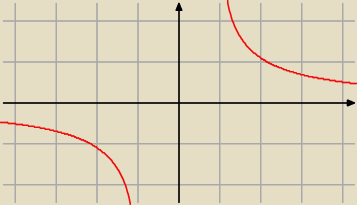
Jack: tak samo jak funkcja tangens jest w przedzialach rosnaca

Adamm: