;; Brzusiu Kiełbasiany: Znaleźć macierz symetrii względem prostej o równaniu 2x + 5y = 0 z użyciem wartosci wlasnych i wektorow wlasnych, wzoru PDP⁻¹ Sęk w tym, że zrobiłem, ale mam rozwiązanie, i nie pokrywa się z nim. Coś mi się od dwoch godzin nie zgadza, dlatego wysylam tutaj.

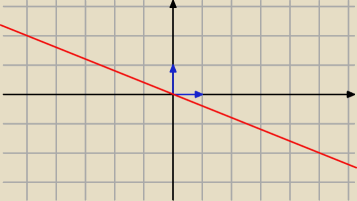
Adamm: bierzemy wektor na prostej v=[5, −2] i'=[x, y] i'•v=5x−2y=5 5x−5=2y 25x²−50x+25=4y² 25x²−50x+25=4−4x² 29x²−50x+21=0

	21
x=1 lub x=
	29

(x=1 to i)

	20
y=−
	29

	21		20
i'=[		, −		]
	29		29

j'=[x', y'] −j'•v=2y'−5x'=2 4y'²=25x'²+20x'+4 4−4x'²=25x'²+20x'+4 0=29x'²+20x'

	20
x'=0 (wersor j) lub x'=−
	29

	21
y'=−
	29

	20		21
[P[j']=[−		, −		]
	29		29

	21/29 −20/29 −20/29 −21/29		1	21 −20 −20 −21
M=		=
			29