kwadraty

kwadraty kotoś: Kwadrat ABCD jest wpisany w kwadrat EFGH. Niech A' bedzie odbiciem punktu A wzgledem C. Wiedząc że AB=6, oblicz maksymalną długość A'E.

25 gru 20:30

Qulka: max to 18

25 gru 20:38

kotoś: Mozesz objaśnić?

25 gru 20:39

kotoś:

25 gru 21:29

5-latek: Witam emotka

czy zmienilas adres email ?

25 gru 21:34

kotoś: co?

25 gru 21:38

5-latek: To nie bylo do Ciebie .

25 gru 21:40

kotoś: To po co piszesz w moim temacie?

25 gru 21:43

5-latek: Bo tak mi bylo wygodnie .

25 gru 21:44

Qulka: witaj 5 latku..nie, ale nieczęsto zaglądam emotka

25 gru 21:53

kotoś: Dziwne tu panują zasady.

25 gru 21:53

Qulka: jednak max jest trochę większy ... około 18.25

25 gru 21:54

Qulka: http://www.wolframalpha.com/input/?i=max+36*sin(a)%2B288-144%E2%88%9A2+*sin(a)*cos(3Pi%2F4-a)+from+0+to+pi%2F2

25 gru 21:55

Qulka: z twierdzenia cosinusów x²= 36*sin(a)+288−144√2 *sin(a)*cos(3Pi/4−a)

25 gru 21:55

5-latek: Rozumiem emotka

25 gru 21:56

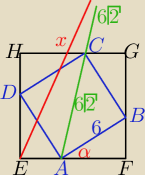
Qulka: rysunek

25 gru 21:58

kotoś: mam to obliczyc normalnie, bez kalkulatorów

25 gru 22:05

Qulka: to policz pochodną i porównaj z zerem emotka

25 gru 22:10

Qulka: albo policz dla tych które znasz 0°, 30°, 45°, 60° , 90° i okaże się że dla 30° jest prawie max

25 gru 22:17

Qulka: sorry..zapomniałam kwadratu przy pierwszym sinusie ... max = 18

25 gru 22:26

Qulka: x²= 36*sin²(a)+288−144√2 *sin(a)*cos(90°−a+45°)

25 gru 22:28