okręgi Wilku: Dwa okręgi o tym samym promieniu r przecinają się w punktach A i B. Współna styczna ma punkty styczności M i P. Oblicz promień okregu opisanego na APM.

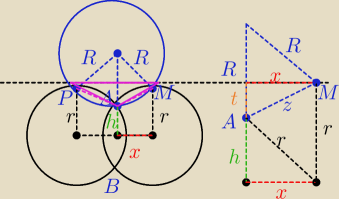
iteRacj@: r − długość promieni wyjściowych okregów R − długość promienia okręgu opisanego na Δ APM x − połowa odległości między środkami wyjściowych okregów z tw. Pitagorasa h²=r² − x² h+t=r t=r−h t= r−√r²−x² z tw. Pitagorasa R²=(R−t)²+x² R²=R²−2R*t+t²+x² 2R*t=t²+x²

	t2+x2
2R=
	t

	( r−√r2−x2)2+x2
2R=
	r−√r2−x2

	( r2−2r*√r2−x2)2+r2−x2+x2
2R=
	r−√r2−x2

	( r2−r*√r2−x2)
R=		=r
	r−√r2−x2

R=r − długość promienia okręgu opisanego na Δ APM jest równa długości promieni wyjściowych okregów