pochodna maciej: cześć mam pewien problem, badam przebieg zmienności funkcji.y=e^x_x−1 ,ale pierwsza pochodna nie ma miejsc zerowych i nie wiem jak zbadać monotoniczność,proszę o podpowiedź jak sobie z tym poradzić

Janek191: Napisz porządnie funkcję

maciej:

	x
y=e do potęgi
	x−1

jc: Funkcja x →e^x jest funkcją rosnącą.

	x		(x−1)+1		1
Wystarczy więc badać funkcję x →		=		=1+		.
	x−1		x−1		x−1

Ta druga funkcja maleje na każdym z przedziałów (−∞,1) i (1,∞), ale nie na sumie. To samo można powiedzieć o Twojej funkcji.

maciej: Zastanawiam się dlaczego w tabelce przy zmienności funkcji w dopowiedział w sekcji zarezerwowanej dla f(x)'. są same minusy,oznacza to że funkcja jest malejąca,ale po wrzuceniu wykresu pochodnej do geogebry wyskakuje że funkcja rośnie od −∞do 0,5 a później już tylko maleje

maciej: w odpowiedziach*

maciej: jeżeli mam narysować wykres ta muszę wiedzieć w jakich przedziałach pochodna jest −/+

jc: Bo jest malejąca. Pomyliłem słowa.

jc:

	1
Dla x > 1, jak weźmiesz większe x, to wyrażenie 1+		zmniejszy się.
	x−1

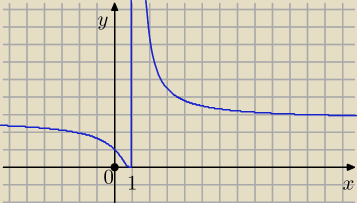
Dla x < 1 podobnie, ale liczby są ujemne, więc moment trzeba pomyśleć. Można w ogóle nie myśleć, tylko wyobrazić sobie wykres, czyli hiperbolę.

maciej: nie potrafię wysnuć wniosków apropos tej pochodnej z twojej wypowiedzi

jc: Pochodna powinna być ujemna, ale monotoniczność widać bez liczenia pochodnej. Zwróć uwagę, że funkcja nie jest monotoniczna na całej dziedzinie. f(0)=1, f(2)=e², f(0)<f(2).

Janek191: