ZAD omikoron: W trójkącie ABC poprowadzono środkową CD i wyznaczono na niej taki punkt E,tak ,ze |CE|/|ED|=1/3 Prosta przechodząca przez punkty AE przecina bok BC w punkcie P. Wykaż, że |CP|/|PB|=1/6

omikoron: dziekuje za wcześniejszą pomoc

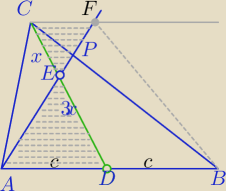
Mila: CF||AB 1) ΔCFE∼ΔADE⇔

CF		CF		1
	=		=
AD		c		3

	CF		1
2) ΔCFP∼ΔABP w skali k=		=		⇔
	2c		6

CP		1
	=
PB		6

lpom: dzięki za pomoc

jc: Algebraicznie.

	3		1		3		1		1		1
E=		C +		D =		C+		(		A +		B)=
	4		4		4		4		2		2

1		1		3		1		7		1		6
	A +		B+		C=		A +		(		B+		C),
8		8		4		8		8		7		7

	1		6
czyli P=		B+		C, co oznacza, że CP:BP=1:6.
	7		7