zad omikoron: Ciąg an= a,4,b,c jest arytmetyczny, a ciąg an= a,a+b,4c jest geometryczny. Oblicz a, b i c.

Jerzy: Jak to widzisz ?

omikoron: a+c/2=4+b c aryt. (a+b)²=4ac c geom.

Jerzy: Ej.... w takim razie dobrze przepisałeś treść zadania ?

omikoron: tak oprocz tego ,ze są w nawiasach

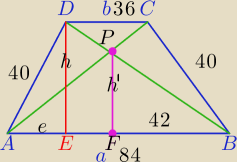
omikoron: W trapezie równoramiennym ABCD, w którym AB CD || , dane są AB = 84 , CD = 36 , BC AD = = 40 . Oblicz promień okręgu wpisanego w trójkąt ABP, gdzie P jest punktem przecięcia przekątnych tego trapezu.

omikoron: to jak zrobic te pierwsze zadanie ?

Jerzy: Skąd wniosek co do ciągu arytmetycznego ?

omikoron: a+b/2=4 i 4+c/2=b ?

Jerzy:

omikoron: dzieki dalej dam radę

omikoron: a na drugie masz pomysł ?

omikoron: z trapezem ?

omikoron: up

omikoron: Dany jest wielomian ( ) 3 ( ) 3 1 9 20 4 3 2 2 2 W x = x − mx + m − x − m + m + . Wykres tego wielomianu, po przesunięciu o wektor u = −[ 3, 0]  , przechodzi przez początek układu współrzędnych. Wyznacz wszystkie pierwiastki wielomianu W.

omikoron: Trzy liczby tworzą ciąg arytmetyczny. Jeśli do pierwszej z nich dodamy 5, do drugiej 3, a do trzeciej 4, to otrzymamy rosnący ciąg geometryczny, w którym trzeci wyraz jest cztery razy większy od pierwszego. Znajdź te liczby. prosze o pomoc w tym zadaniu

Mila: P_ΔABP=p*r=a*h' 1) e=(84−36):2=24, |EB|=60 2) W ΔDEB: 40²=24²+h² h²=1024 h=32

	60		10
ΔDEB∼ΔPFB w skali k=		=
	42		7

h		10		32		10
	=		⇔		=
h'		7		h'		7

	112
h'=		=22.4
	5

3) W ΔPFB: |PB|²=42²+22.4²⇔|PB|=47.6

	1
PABP=		*84*22.4=940.8
	2

	2*47.6+84
PABP=		*r=89.6*r
	2

940.8=89.6*r r=10.5 ==== posprawdzaj rachunki, albo odpowiedź

omikoron: Reszta z dzielenia liczby naturalnej a przez 6 jest równa 1. Reszta z dzielenia liczby naturalnej b przez 6 jest równa 5. Uzasadnij, że liczba 2 2 a b − jest podzielna przez 24. nie wiem z ktorej strony je zaczac

Mila: 22*ab ma być podzielna przez 24? Coś źle zapisane?

ford: Trzy liczby tworzą ciąg arytmetyczny. Jeśli do pierwszej z nich dodamy 5, do drugiej 3, a do trzeciej 4, to otrzymamy rosnący ciąg geometryczny, w którym trzeci wyraz jest cztery razy większy od pierwszego. Znajdź te liczby. prosze o pomoc w tym zadaniu ========================================= rosnący ciąg geometryczny, w którym trzeci wyraz jest cztery razy większy od pierwszego a₃ = 4*a₁ a₁*q² = 4*a₁ ||a₁ q² = 4 q = 2 (a, 2a, 4a) − ciąg geometryczny (a−5, 2a−3, 4a−4) − ciąg arytmetyczny

	a−5+4a−4
2a−3 =
	2

	5a−9
2a−3 =		|*2
	2

4a−6 = 5a−9 a = 3 (3−5, 2*3−3, 4*3−4) = (−2, 3, 8) − ciąg arytmetyczny Szukane liczby to (−2), 3 i 8

omikoron: Reszta z dzielenia liczby naturalnej a przez 6 jest równa 1. Reszta z dzielenia liczby naturalnej b przez 6 jest równa 5. Uzasadnij, że liczba a²−b²− jest podzielna przez 24.

omikoron: dzieki ford ,ale to już wiedziałam

omikoron: Mila mogłabym prosić o wytłumaczenie ?

omikoron: zadania z resztą

Mila: Za pół godziny będę na forum. Tymczasem sprawdź 18:42.

omikoron: W ostrosłupie prawidłowym czworokątnym ABCDS o podstawie ABCD wysokość jest równa 5, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę 120°. Oblicz objętość tego ostrosłupa. w tym zadaniu prosiłabym o odpowiedz czy to V=160 ?

Mila: a=6k+1 b=6m+5 k,m∊N a²−b²=(a−b)*(a+b)=(6k+1−6m−5)*(6k+1+6m+5)= =(6k−6m−4)*(6m+6k+6)=12*(3k−3m−2)*(m+k+1) Jeden z czynników jest podzielny przez dwa zatem a²−b² jest podzielny przez 24

Mila: d=10√2 a=10

	500
V=		[j3]
	3

omikoron: Na boku AB trójkąta równobocznego ABC wybrano punkt D taki, że AD DB : 2:3 = . Oblicz tangens kąta ACD .

omikoron: dzięki za wcześniejsze zadania

Mila: |AD|=0.4a 1) CD z tw. cosinusów 2) tw. sinusów 3) jedynka tryg.

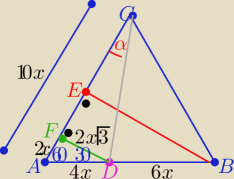
Eta: Podaję jeden ze sposobów: 1/ Na rys. dorysowuję wysokość BE i równoległy do niej odcinek DF trójkąt ADF "ekierka" to |FD|=2x√3 i |AF|=2x to |FC| =8x

	|FD|		2x√3		√3
W ΔDFC tgα=		=		=
	|FC|		8x		4

=======

omikoron: Krawędź podstawy ostrosłupa prawidłowego czworokątnego ABCDS ma długość a. Ściana boczna jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem 2α . Ostrosłup ten przecięto płaszczyzną, która przechodzi przez krawędź podstawy i dzieli na połowy kąt pomiędzy ścianą boczną i podstawą. Oblicz pole powstałego przekroju tego ostrosłupa.

Adam: A omikoron tylko przepisuje

omikoron: a kto ty ,że prawo głosu masz ?

matma: https://www.zadania.info/d171/5639561

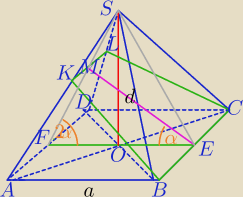
Mila: 1) W ΔSOF:

	1   a 2
cos(2α)=
	|SF|

	a
|SF|=		=|SE|
	2cos(2α)

2) Z tw, sinusów w ΔFEM:

|FM|		|EF|
	=
sinα		sin(180−3α)

	a*sinα
|FM|=
	sin(3α)

d		a
	=
sin(2α)		sin3α

	a*sin(2α)
d=
	sin(3α)

=============== 3)W ΔSEM:

MS|		d
	=
sinα		sin(180−4α)

	a*sinα
|MS|=
	2cos(2α)*sin(3α)

4) ΔSKL∼ΔADS:

|KL|		|SM|
	=
a		|SF|

	a		a*sinα
|KL|*		=a*
	2cos(2α)		2cos(2α)*sin(3α)

	asinα
|KL|=
	sin(3α)

5) Licz pole trapezu

Mila: Szkoda, że nie widziałam, że rozw. jest w info. Trochę chyba inaczej rozwiązywałam. Dokończ. Omikron

Adam: Czemu usunełaś mój post Mila To taki żart tylko

Mila: Dobry żart jest tynfa wart