Oblicz przekatne i pole Yes of course: Dany jest równoległobok ABCD, w którym boki mają długość 2 cm i 6 cm, a pole wynosi 8 cm2. Oznaczmy środki boków AB i BC odpowiednio jako punkty P i Q. Oblicz długości przekątnych równoległoboku ABCD oraz pole czworokąta APQD

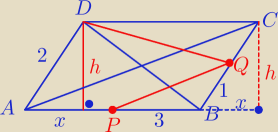
Janek191: a = I AB I = 6 cm Pole

	4
P = a*h = 6 h = 8 ⇒ h =
	3

	4
h =		cm
	3

	16		36 − 16		20
Mamy x2 = 22 − h2 = 4 −		=		=
	9		9		9

	2 √5
x =
	3

p₁ = I AC I (p₁)² = ( 6 + x)² + h² = ... oraz p₂ = I BD I ( p₂)² = ( 6 − x)² + h² = ... Pole ΔPBQ

	2
P1 = 0,5*3* 0,5 h = 1,5*		= 1 [cm2]
	3

Pole ΔCDQ

	2
P2 = 0,5*6*0,5 h = 3*		= 2 [ cm2]
	3

więc pole czworokąta APQD jest równe P =( 8 − 1 − 2) cm² = 5 cm²

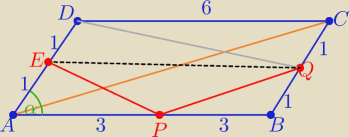Eta: P(ABCD)=8 ⇒ P(ABC)=4 trójkąty PBQ i ABC są podobne w skali k=1/2 to P(PBQ)=4*k² ⇒ P(PBQ)=1 i P(APE)=P(PBQ)=1 to P(EPQ)=P(DEQ= 2 zatem P(APQD)= 1+2+2=5 [cm²] ======================= Długości przekątnych wyznaczamy z tw. cosinusów w trójkątach ABC i ABD najpierw wyznaczamy sinα w ΔABE

	1		2		√5
P(APE)=		*3*1*sinα =1 ⇒ sinα=		to cosα=√1−sin2α= .... =
	2		3		3

i teraz: |BD|²=6²+2²−2*6*2*cosα=............ |AC|²= 6²+2²+2*6*2*cosα=..............