PP i wypuklosc wojtek: . Określić przedziały wypukłości oraz punkty przegięcia wykresu funkcji:

x3
x2+12

da się to jakoś zrobić bez paru stron rachunków?

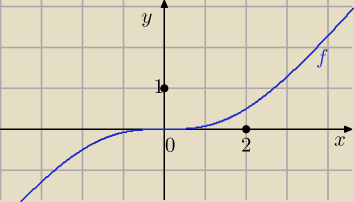
Janek191: f(x) = U{x³}{x² + 12| więc

	3 x2*(x2 +12) − x3*2 x		3 x4 + 36 x2 − 2 x4
f '(x) =		=		=
	(x2 + 12)2		(x2 +12)2

	x4 + 36 x2
=
	x4 + 24 x2 + 144

więc

	4 x3*(x4 +24 x2 +144) − x4*(4 x3 + 48 x)
f ''(x) =		=
	(x4 + 24 x2 + 144)2

	4 x7 + 96 x5 + 576 x3 − 4 x7 − 48 x5
=		=
	( x2 + 12)4

	48 x5 + 576 x3		x3*( 48 x2 + 576)
=		=
	(x2 + 12)4		(x2 + 12)4

Dla x < 0 jest f ''(x) < 0 więc funkcja f jest wklęsła, Dla x > 0 jest f ''(x) > 0 więc funkcja f jest wypukła, Dla x = 0 jest f ''(x) = 0 więc w x =0 funkcja f ma punkt przegięcia.

jc:

x3		x(x2+12)−12*x		12x
	=		=x −
x2+12		x2+12		x2+12

Teraz łatwiej różniczkować.

jc:

	2x(x2−36)
Druga pochodna = −
	(x2+12)3

Teraz badaj znak (x−6)x(x+6).

wojtek: dlaczego w f'' pominąłeś 36x²?

jc: W rachunku niechcący pominąłem czynnik 12 w liczniku, ale to nie wpływa na znak.

jc:

	x(x2−36)
Poprawny wynik = − 24		.
	(x2+12)3

wojtek: ale pytałem janka dlaczego w 2 pochodnej w liczniku pominał 36x²

Janek191: Zagapiłem się

wojtek: okej policzylem i w liczniku jest 3x⁷ − 24x⁵ −1152x³ +1728x i teraz jak to przyrownac do zera to pae stron rachunkow co ja powiem profesorowi xD

5-latek: Ze za duzo rachunkow i nie bedziesz tyle liczyl jak chce to niech sobie sam policzy i juz .

jc: wojtek, to nie jest taki straszny rachunek.

x3		x
	=x−12
x2+12		x2+12

	x
Wystarczy, że zróżniczkujesz		.
	x2+12

[x(x²+12)⁻¹]' = (x²+12)−2x²(x²+12)⁻² = (12−x²)(x²+12)⁻² [(12−x²)(x²+12)⁻²] = −2x(x²+12)⁻² − (12−x²)4x(x²+12)⁻³ = −2x[x²+12 + 2(12−x²)](x²+12)⁻³= 2x(x²−36)(x²+12)⁻³

jc: W drugiej linijce zgubiłem prim za nawiasem [ ].

jc: Jeszcze prościej.

2x		1		1
	=		+
x2+12		x+i√12		x−i√12

	2		2		4(x3−36x)
Druga pochodna =		+		=
	(x+i√12)3		(x−i√12)3		(x2+12)3

jc: Spodobało mi się to zadanie

5-latek: Dobry wieczor jc Bo to pewnikiem Ty je zadales

jc: Na pewno nie ja. Nie lubię takich zadań. Jak się nie wie, jak liczyć, to można się zaliczyć.

	x3
Ogólnie: f(x)=		, a>0.
	x2+a

x3		x(x2+a)−ax		ax		a/2		a/2
	=		=x −		= x −		−		.
x2+a		x2+a		x2+a		x+i√a		x−i√a

	a		a		x3−3ax
Druga pochodna = −		−		= −2a
	(x+i√a)3		(x−i√a)3		(x2+a)3

wojtek: jc (x(x²+12) −12x)/(x²+12)

	12x
to nie powinno być 1 −		? i z tego pochodną pierwszą i drugą?
	x2+12

jc: Nie, tam powinno być x − ... , ale to nie ma znaczenia. x''=0.

wojtek: nie rozumiem tak to dlaczego myslałem że

jakaś liczba
	= 1
jakaś liczbye

jc: x(x²+12)/(x²+12)=x, a nie jeden.

Mi: A dobra sorry dopiero teraz zauważyłem to xD za dużo matmy dzisiaj i takich błahostek nie dostrzegam