Geometria-pytanie
kosta: Łatwe pytanie do geometrii analitycznej− mam za zadanie zilustrować w układzie współrzędnych
zbiór A:
A={(x,y): x
2+y
2+2x>0}
Wychodzi więc (x+1)
2+(y−0)
2=1
Czyli okrąg o środku o współrzędnych (−1,0) i o promieniu 1. Jednak skoro w poleceniu jest >0,
to jak mam to narysować?
Tylko 'górną' część koła, która jest powyżej OX? takie półkole? Byłabym wdzięczna za
odpowiedź

20 gru 15:54
iteRacj@:
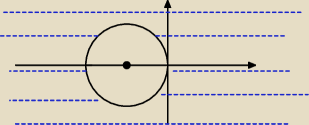
(x+1)
2+(y−0)
2>1
jest to zbiór punktów, które są odległe od środka okręgu o więcej niż 1
czyli
zewnętrze okręgu
20 gru 16:15
Mila:
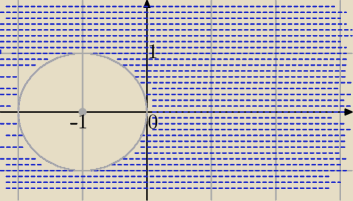
20 gru 16:21
kosta: Rozumiem, dzięki, mam jeszcze pytanie do kolejnego podpunktu, mam taki zbiór:
A={(x,y): −3x2+6x+1≥3y2+12y+4}
Więc 3y2+12y+4 +3x2−6x−1≤0
Wyszło mi: (√3y+2√3)2 + (√3x−√3)2=12 Więc środek okręgu= (−2√3, √3), promień=
2√3
Skoro mniejsze/równe zero to zamalowałabym cały okrąg, jednak w odpowiedziach jest okrąg o
środku (1,−2) i promieniu 2, gdzie popełniłam błąd?
20 gru 16:30
kosta: Ah chyba rozumiem, mam zapisać równanie w postaci (y−...)2+(x−....)2, tak? Tzn NIE mogę
napisać √3y, jest to błąd, tak?
20 gru 16:32
Mila:
−3x2+6x+1≥3y2+12y+4
−3x2+6x+1−3y2−12y−4≥0 ⇔−3x2+6x−3y2−12y−3≥0 /:(−3)
x2−2x+y2+4y+1≤0
(x−1)2−1+(y+2)−4+1≤0
(x−1)2+(y+2)2≤4
S=(1,−2), r=2
Koło.
20 gru 16:49

 (x+1)2+(y−0)2>1
jest to zbiór punktów, które są odległe od środka okręgu o więcej niż 1
czyli zewnętrze okręgu
(x+1)2+(y−0)2>1
jest to zbiór punktów, które są odległe od środka okręgu o więcej niż 1
czyli zewnętrze okręgu
