bardzo trudne Maciek: Dany jest trójkąt równoramienny ABC o podstawie |AB|=2a i kątach przy podstawie równych α Na ramionach tego trójkąta zbudowano dwa trójkąty równoramienne AEC i BFC o podstawach które są ramionami trójkąta ABC Kąty przy podstawach tych trójkątów są równe α/2 Wiedząc,że suma pól tych trójkątów jest dwa razy większa od pola trójkąta ABC wyznacz wartość cosiusa kąta α Pomoże ktoś bardzo proszę

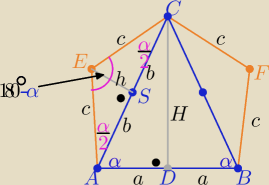
Eta: 1/ poprawny rysunek zgodny z treścią zadania

	1		c2		1
P(AEC)=P(BFC)=		c*c*sin(180o−α)=		sinα i P(ABC)=		*2a*2b*sinα=2absinα
	2		2		2

z treści zadania

	b		b		α
c2sinα=absinα ⇒ c2=ab / :c ≠0 ⇒ c= a		i w ΔASE		= cos
	c		c		2

	α		α		c2		α
to c= a*cos		⇒ c2=a2cos2		to b=		⇒ b=a*cos2
	2		2		a		2

	a		α
W ΔADC cosα=		⇒ a=2b*cosα ⇒ a=2acos2		*cosα /:a≠0
	2b		2

	α
2cos2		*cosα=1
	2

	α
ze znanej tożsamości 2cos2		=1+cosα
	2

otrzymujemy: (1+cosα)*cosα=1 ⇒ cos²α+cosα−1=0 Δ=......................... i cosα>0

	√5−1
cosα=
	2

=============

Mila: Maciek, jak zwykle popatrzy za trzy dni.

Maciek: Eta bardzo, bardzo dziękuję

Mila: No i pięknie.