Prawdopodobieństwo A: Eta, bardzo proszę Cię o pomoc 1.Losujemy dwie karty spośród 6 (dwie dwójki, trzy trójki i jedna czwórka). Przyjmijmy, że wynik losowania to suma liczb na kartach. Dla każdego z możliwych wyników oblicz prawdopodobieństwo otrzymania tego wyniku. 2. W każdej z urn jest 6 kul czarnych, 4 kule czerwone i 5 kul białych. Oblicz prawdopodobieństwo tego, że losując po jednej kuli z każdej urny, wyciągniemy dwie kule tego samego koloru.

justka:

	6 2
|Ω| =		= 15

A − " suma wylosowanych liczb wynosi − 4"

	2 2
|A|=		= 1

P(A) = 1/15 B−"suma wylosowanych liczb wynosi − 5"

	2 1		3 1
|B| =		*		= 6

P(B) = 6/15 C −" = suma wylosowanych liczb wynosi − 6"

	3 2		2 1		1 1
|C| =		+		*		= 3+ 2 = 5

P(C) = 5/15 D− "suma wylosowanych liczb wynosi − 7" |D| = {3}{1}*{1}{1} = 3 P(D) = 3/15

justka: Ile jest urn w zadaniu 2?

A: dwie

Eta: Dzięki justka Nie było mnie przez chwilę przy kompie.

A: Eta, mam problem z rozrysowaniem tego drugiego zadania za pomocą drzewka. Niby coś obliczyłam, ale mam problem wielki

justka:

	5
a =
	15

	6
b =
	15

	4
c =
	15

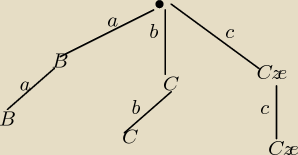
D− " wylosujemy dwie kule tego samego koloru"

	5		5		6		6		4		4
P(D) =		*		+		*		+		*		=...
	15		15		15		15		15		15

Eta: A={ ( cz, cz) ( c, c) ( b,b)} P(cz)= ⁶₁₅ P(c)= ⁴₁₅ P(b)= ⁵₁₅ to P(A) = ⁶₁₅*⁶₁₅ + ⁴₁₅*⁴₁₅ + ⁵₁₅*⁵₁₅=......

A: A w tym pierwszym drzewko? Przepraszam, że was tak męczę, ale chyba powoli łapię o co w tym chodzi.

justka: Też można narysować

A: Mogłaby mi któraś z was jeszcze do 1 drzewko narysować? To już będę miała dwa porządne przykłady jak to robić.

Eta: w zimie drzewka są zasypane śniegiem nie do każdego zad. jest potrzebne drzewko

A: Wiem, ale mój nauczyciel tego wymaga do tych zadań, a ja mam problem z ich rysowaniem