Wyznacz objętość tego ostrosłupa i oblicz cos kąta nachylenia krawędzi bocznej Danio: Podstawą ostrosłupa jest trójkąt równoramienny którego kąt miedzy równymi bokami wynosi 45 stopni a długość podstawy tego trójkąta wynosi a.Wysokość ostrosłupa jest równa 2a, a wszystkie krawędzie boczne są nachylone do podstawy pod tym samym kątem.Wyznacz objętość tego ostrosłupa i oblicz cos kąta nachylenia krawędzi bocznej do podstawy.

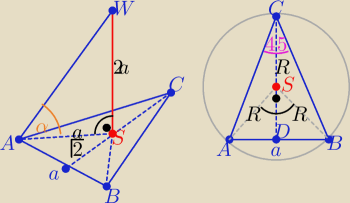
Eta: Jeżeli wszystkie krawędzie boczne są nachylone do podstawy pod tym samym kątem to spodek wysokości ostrosłupa pokrywa się ze środkiem okręgu opisanego na podstawie

	a		a√2
zatem ΔABS jest prostokątny to R=		=
	√2		2

	a
|DS|=|AD|=
	2

	a		a√2		a		a
|CD|=hp= R+		=		+		=		(√2+1)
	2		2		2		2

	1		a2
Pp=		*a*h=		(√2+1)
	2		4

	1		a3
V=		Pp*H= ...........		(√2+1)
	3		6

	a2		3a
W ΔASW |AW|= √4a2+		=
	2		√2

	|AS|		1
cosα=		= .............=
	|AW|		3

y: Δ

Eta: Czego chcesz?