matematykaszkolna.pl
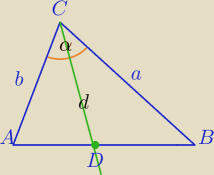
Geometria Lennox: W trójkącie ABC w którym AC=b, BC=a i ∡ACB=α z wierzchołka C poprowadzono dwusieczną kąta,
 2ab*cosα 
która przecięła bok AB w punkcie D. Udowodnij, że CD=
 a+b 
17 gru 18:27
Lennox: Mógłby mi ktoś pomóc?
17 gru 19:03
Eta:
 2abcosα 
Jeżeli w treści jest|∡ACB|=2α to |CD|=
 a+b 
 2ab*cos(α/2) 
Jeżeli w treści jest |∡ACB|=α to |CD|=
 a+b 
Popraw dane w treści zadania
17 gru 19:10
Mila: rysunek
 1 
PΔ=
*a*b*sinα
 2 
1 1 α 1 α 
*a*b*sinα=
*b*d*sin
+
*a*d*sin
⇔
2 2 2 2 2 
 α 
a*b*sinα=d*sin
*(a+b)
 2 
 α α α 
2sin
*cos
*a*b=d*sin
*(a+b)
 2 2 2 
 α 
2cos
*a*b=d*(a+b)⇔
 2 
 
 α 
2a*b*cos
 2 
 
d=
 a+b 
=============
17 gru 19:15
Eta: Wrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrr !
17 gru 19:15
Lennox: Niestety nie mam możliwości poprawienia zadania, gdyż w takiej formie otrzymałem od nauczyciela
17 gru 19:19
Eta: To taka równość nie zachodzi! Powiedz to swojemu Panu emotka
17 gru 19:20
Lennox: Dzięki za rozwianie wątpliwości, już wiem dlaczego nic mi nie wychodziło emotka
17 gru 19:22
Eta: To co podała Mila niestety.... ale nie spełnia treści tego zadania emotka
17 gru 19:23
Martyna: A czy mógłby mi ktoś wytłumaczyć co tu zaszło pomiędzy 3 i 4 pod tym rysunkiem trójkąta
14 sty 19:43
ABC: a co miało zajść ? Eta warczała , normalna sprawa
14 sty 20:25
Martyna: Ale z jakiego wzoru to jest dlaczego z sinusa zrobiło się 2sina/2*cosa/2
14 sty 20:38
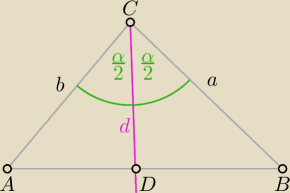
chichi: rysunek
 1 1 α 1 α 
PABC =
ab⋅sin(α), PACD =
bd⋅sin(
), PDCB =
ad⋅sin(
)
 2 2 2 2 2 
no ale sum pól trójkątow ACD i CDB jest równa polu trójkąta ABC, zatem zachodzi równość:
1 1 α 1 α 
ab⋅sin(α) =
bd⋅sin(
) +
ad⋅sin(
) / ⋅ 2
2 2 2 2 2 
 α α 
ab⋅sin(α) = bd⋅sin(
) + ad⋅sin(
)
 2 2 
 α α 
ze wzoru na sinus podwojonego kąta mamy: sin(α) = 2sin(
)cos(
),
 2 2 
 α 
więc wstaw to z lewej strony, podziel stronami przez sin(
), przekształć i masz emotka
 2 
14 sty 20:51
Martyna: Dziękuję chichli
14 sty 21:20