Geometria Madd: W trójkącie KLM, w którym KM = LM = 2a, środkowe poprowadzone z wierzchołków K i L przecinają

	6a2
się pod kątem prostym. Wykaż, że pole trójkąta KLM jest równe P =
	5

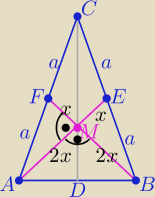Eta: 1/ środkowe dzielą się w stosunku 2:1 licząc od wierzchołka 2/ trzy środkowe dzielą każdy trójkąt na sześć trójkątów o równych polach i jedziemy

	a2
4x2+x2=a2 ⇒ a2=5x2⇒ x2=
	5

	1		6a2
P(ABC)= 6*p(AMF) ⇒P(ABC)= 6*		*2x*x =
	2		5

c.n.w.

Eta: Wprowadź oznaczenia KLM ( bo nie zauważyłam i wpisałam ABC

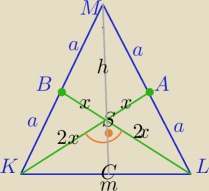Mila: 1) W ΔKSB: a²=x²+(2x)²⇔ a²=5x² 2) WΔKLS: m²=(2x)²+(2x)²⇔m²=8x²

	a2
m2=8*		⇔
	5

	2√2*a
m=
	√5

========== 3) W ΔMCL:

	m		√2*a
(2a)2=(		)2+h2 ⇔4a2=(		)2+h2
	2		√5

	2a2		18
4a2=		+h2 ⇔h2=a2*
	5		5

	3√2
h=a*
	√5

========== 4)

	1
PΔKLM=		*m*h
	2

	1		2√2*a		3√2		6a2
PΔKLM=		*		*a*		=
	2		√5		√5		5

	6a2
PΔKLM=
	5

==============

Madd: Dziękuję

Eta: