
 Podstawą graniastosłupa prostego jest romb o boku a i kącie ostrym α. Dłuższa przekątna
graniastosłupa nachylona jest do podstawy pod kątem β. Oblicz objętość tego graniastosłupa.
Podstawą graniastosłupa prostego jest romb o przekątnych długości a i b. Jedna z przekątnych
graniastosłupa ma długość b. Oblicz objętość tego graniastosłupa?
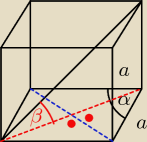
Podstawą graniastosłupa prostego jest romb o boku a i kącie ostrym α. Dłuższa przekątna
graniastosłupa nachylona jest do podstawy pod kątem β. Oblicz objętość tego graniastosłupa.
Podstawą graniastosłupa prostego jest romb o przekątnych długości a i b. Jedna z przekątnych
graniastosłupa ma długość b. Oblicz objętość tego graniastosłupa?

 1)
1)
| 1 |
| |||||||||
sin | α= | |||||||||
| 2 | a |
| 1 | 1 | |||
sin | α * a = | e
| ||
| 2 | 2 |
| 1 | ||
sin | α * 2a = e
| |
| 2 |
| H | ||
tgβ = | ||
| e |
| 1 | ||
H = tgβ* sin | α * 2a
| |
| 2 |
| 1 | 1 | |||
V = Pp*H = a2*sinα*tgβ* sin | α * 2a = 2a3*sinα*tgβ*sin | α
| ||
| 2 | 2 |

| 1 | 1 | |||
zastąp sin | α na cos | α | ||
| 2 | 2 |
| ab | ab√b2−a2 | |||
V = H*Pp = √b2−a2 * | = | |||
| 2 | 2 |
