Wielościany Kasia: Wielościany Krawędź boczna ostrosłupa prawidłowego trójkątnego ma długość a i tworzy z krawędzią podstawy kąt o mierze α. Jaką objętość ma ten ostrosłup?

Kasia: Pomocy

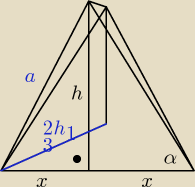Godzio: 2x−krawędź podstawy h−wysokość ściany bocznej H−wyokość ostrosłupa h₁ − wysokośc podstawy

	x
cosα =
	a

x = cosα*a

	2x√3
h1 =
	2

2		2x√3		2cosα*a√3
	h1 =		=
3		3		3

	2
(		h1)2 + H2 = a2
	3

	4cos2α*a2*3
H2 = a2 −
	9

	3a2 − 4cos2α*a2
H2 =
	3

	a√3−4cos2α
H=
	√3

	(2x)2√3		cos2α*a2√3
Pp =		=
	4		4

	cos2α*a2√3		a√3−4cos2α
V = Pp * H =		*		=
	4		√3

cos2α*a3√3−4cos2α
4

sprawdź jeszcze moje obliczenia

Kasia: Dziekuje ci bardzo sprawdzę Gdybyś mogł zobaczyc jeszcze jedno moje zadanie tez z wielościanów będe wdzieczna

Godzio: prosze wyślij mi je tutaj bo nie chce mi się szukać