wyznacz dziedzine funkcji
ja: log13(x2−x4)
2 lut 20:06
Godzio:
x
2 − x
4 > 0
x
2(1−x
2) > 0
x
2(x
2−1) < 0
x
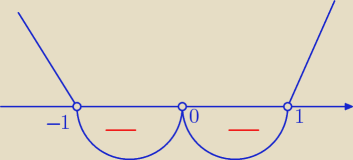
2(x−1)(x+1) < 0
x=0 v x=1 v x=−1
x∊(−1,0) ∪ (0,1)
2 lut 20:11
vega:
logab , to b>0 i a>0 i a ≠1
D: x2 −x4 >0 => x2( 1−x2)>0 => x2( 1−x)(1+x) >0
x2 >0 dla każdego x€R\{0}
(1−x)(1+x) >0 => x€( −∞, −1) U ( 1, ∞)
D= ( −∞,−1)U ( 1, ∞) , bo x =0 nie należy do tego przedziału
2 lut 20:12
vega:
O .o sorry x€ ( −1, 1) . bo ramiona paraboli do dołu
więc
D= (−1,1) \ {0}
tak
Godzio podał poprawną odp.
2 lut 20:15
Godzio: vega
przykład z twojej D
x=2
4 − 16 = −12
2 lut 20:15