Nierówność Trygonometryczna Gibon: Rozwiąż nierówność dla x∊<−2π;2π> sinxcosx<√3/4

the foxi: sinxcosx<√3/4 2sinxcosx<√3/2 sin2x<√3/2 ...

Gibon: Właśnie do takiej postaci doszedłem, ale coś mi nie wychodzi wynik, może rozpiszę sin2x<√3/2 t=2x sint<√3/2 t∊(4π/3+2kπ;5π/3+2kπ) x∊(2π/3+kπ;5π/6+kπ) Czy popelniłem tutaj jakiś błąd?

Gibon: Oczywiście nie brałem jeszcze pod uwage przedziału w którym rozwiązuje, chodzi mi tlyko o to czy d o tego momentu wszystko jest ok.

Mila:

	√3
sin(2x)<
	2

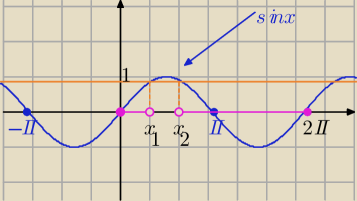
Rozwiązanie w przedziale <0,2π>

	π		2π
0≤2x<		lub		<2x≤2π
	3		3

W takim razie , uwzgledniając okresowość sinusa:

	π		2π
0+2kπ≤2x<		+2kπ lub		+2kπ<2x≤2π+2kπ /:2
	3		3

	π		π
kπ≤x<		+kπ lub		+kπ<x<π+kπ
	6		3

Masz znaleźć rozwiązania z przedziału <−2π,2π>

	π		π
k=0⇔ 0≤x<		lub		<x<π
	6		3

	7π		4π
k=1⇔π≤x<		lub		<x<2π
	6		3

k=−1 itd

Gibon: Bardzo dziekuje za odpowiedź