Funkcja wymierna Tomek:

	12
Wyznacz wartości parametru m, dla których równianie		− 3 =m2 ma dwa rozwiązania
	|x| +2

. Proszę o pomoc i wytłumaczenie

===:

	12
1. Narysuj f(x)=		−3
	x+2

2.To co po prawej stronie 0y (dodatnie wartości argumentu) pozostaje a dla ujemnych x lustrzane odbicie 3. "tnij" poziomą y=m²

Tomek: Narysował wykres, jednak nie wiem jak później odczytać te wartości dokładnie po narysowaniu y=m²

the foxi: Narysuj prostą równoległą do osi ox i "przemieszczaj" ją w górę i w dół, po czym odczytaj dla jakich wartości y ma ona dwa punkty wspólne z wykresem f(x). Te wszystkie wartości to m², potem chyba wiesz co robić, żeby otrzymać m?

Tomek: Nie rozumiem tylko, dlaczego m² jest prostą, a nie parabolą

the foxi: m jest tylko parametrem, a Twój układ współrzędnych ma osie oy i ox (a nie om) mx² byłoby parabolą, tak samo m²x², ale m to po prostu prosta równoległa do osi ox (funkcja liniowa ax+b, gdzie a=0)

Eta:

	12
y=		−3 , x≠ −2
	x+2

	12
y=		−3
	|x|+2

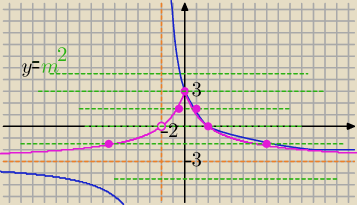y= m² 0 rozwiązań dla m²>3 ⇒ m∊(−∞, −√3) U (√3,∞) 1 rozwiązanie dla m²=3 ⇒ m= −√3 v m= √3 2 rozwiązania dla m²<3 i m²>−3 ⇒ m∊(−√3, √3)

Tomek: Jeszcze jedno pytanie: skoro w mianowniku jest |x| +2 to dziedziną jest zbiór liczb rzeczywistych, ponieważ |x|≠−2 zawsze, tak? Wiec dlaczego w wykresie dla −2 funkcja nie przyjmuje wartości ?

Eta: Tak masz rację D_f= R ... źle spojrzałam Na wykresie różowym tam gdzie x= −2 powinno być kółeczko zamalowane

Tomek: Ok, wszystko juz rozumiem, dziękuje za pomoc

Eta:

===: ... tyle, że m² to zawsze większe od 0 Odpowiedż końcowa dobra ... zapis nie całkiem